练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知是等比数列前20项的和为21，前30项的和为49，则前10项的和为（　　）
    A．7B．9C．63D．7或63
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    2、已知是等比数列前20项的和为21，前30项的和为49，则前10项的和为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知是等比数列前20项的和为21，前30项的和为49，则前10项的和为


    1. A.
      7
    2. B.
      9
    3. C.
      63
    4. D.
      7或63

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知是等比数列前20项的和为21，前30项的和为49，则前10项的和为（　　）
    A．7B．9C．63D．7或63

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年云南省昆明八中高一（下）期中数学试卷（解析版） 题型：选择题

    已知是等比数列前20项的和为21，前30项的和为49，则前10项的和为（ ）
    A．7
    B．9
    C．63
    D．7或63

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知{an}是等差数列．

    (1)前四项和为21，末四项和为67，且各项和为286，求项数；

    (2)Sn＝20，S2n＝38，求S3n；

    (3)若两个等差数列的前n项的和之比是(7n＋1)∶(4n＋27)，求它们的第11项之比．

    查看答案和解析>>

    科目：高中数学 来源：上海模拟题 题型：解答题

    已知点P（a1，b1），P2（a2，b2），...，Pn（an，bn）（n为整数）都在函数y=的图像上，且数列{an}是a1=1，公差为d的等差数列。
    （1）证明：数列{bn}是公比为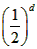的等比数列；
    （2）若公差d=1，以点Pn的横、纵坐标为边长的矩形面积为Cn，求最小的实数t，若使Cn<t（t∈R，t≠0）对一切正整数k恒成立；
    （3）对（2）中的数列{an}，对每个正整数k，在ak与ak+1之间插入2k-1个3（如在a1与a2之间插入20个3，
    a2与a3之间插入21个3，a3与a4之间插入22个3，依此类推），得到一个新的数列{dn}，设Sn是数列
    {dn}的前n项和，试求S1000。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点P1（a1，b1），P2（a2，b2），…，Pn（an，bn）（n为正整数）都在函数y=(
    1
    2
    )x    的图象上，且数列{an} 是a1=1，公差为d的等差数列．
    （1）证明：数列{bn} 是公比为(
    1
    2
    )d    的等比数列；
    （2）若公差d=1，以点Pn的横、纵坐标为边长的矩形面积为cn，求最小的实数t，若使cn≤t（t∈R，t≠0）对一切正整数n恒成立；
    （3）对（2）中的数列{an}，对每个正整数k，在ak与ak+1之间插入2k-1个3（如在a1与a2之间插入20个3，a2与a3之间插入21个3，a3与a4之间插入22个3，…，依此类推），得到一个新的数列{dn}，设Sn是数列{dn}的前n项和，试求S1000．

    查看答案和解析>>


    同步练习册答案