练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在图中，∠1与∠2是同位角的有（　　）

    魔方格
    A．①，②B．①，③C．②，③D．②，④
    B
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：不详 题型：单选题

    在图中，∠1与∠2是同位角的有（　　）

    精英家教网
    A．①②B．①③C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    在图中，∠1与∠2是同位角的有（　　）

    精英家教网
    A．①，②B．①，③C．②，③D．②，④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

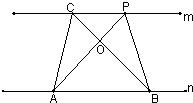    21、如图，已知：直线m∥n，A，B为直线n上两点，C、P为直线m上两点．
    （1）如果A、B、C为三个定点，点P在直线m上移动，那么，无论P点移动到任何位置，总有
    △APB
    与△ABC的面积相等．理由是：
    同底等高的三角形面积相等
    ．
    （2）请写出（1）中其余几对面积相等的三角形：
    △ACP与△BCP、△AOC与△BOP
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

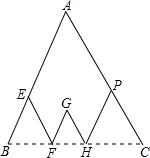
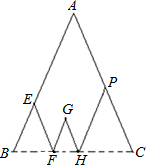    如图，某课题学习小组对地图上的A、B、E、F、G、H、P、C八处地点进行观察、分析．在讨论中得到了∠B=∠C=60°，B、F、H、C都在线段BC上，EF∥GH∥AC，PH∥GF∥AB的正确结论．接着又有两位同学各自提出了如下一个结论：
    甲：△ABC、△BEF、△FGH、△HPC均为等边三角形．
    乙：线路B→A→C与线路B→E→F→G→H→P→C一样长．
    （1）请分别指出甲、乙两位同学的结论是否正确？
    （2）将（1）中你认为正确的结论给予证明？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，某课题学习小组对地图上的A、B、E、F、G、H、P、C八处地点进行观察、分析．在讨论中得到了∠B=∠C=60°，B、F、H、C都在线段BC上，EF∥GH∥AC，PH∥GF∥AB的正确结论．接着又有两位同学各自提出了如下一个结论：
    甲：△ABC、△BEF、△FGH、△HPC均为等边三角形．
    乙：线路B→A→C与线路B→E→F→G→H→P→C一样长．
    （1）请分别指出甲、乙两位同学的结论是否正确？
    （2）将（1）中你认为正确的结论给予证明？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知图①～④，

    在上述四个图中，∠1与∠2是同位角的有（　　）

    查看答案和解析>>

    科目：初中数学 来源：2013年河北省衡水市五校联考中考数学调研试卷（解析版） 题型：解答题

    如图1，在平面直角坐标系中，四边形OABC是梯形，BC∥AO，顶点O在坐标原点，顶点A（4，0），顶点B（1，4），动点P从O点出发，以每秒1个单位长度的速度沿OA的方向向A运动，同时，动点Q从A出发，以每秒2个单位长度的速度沿A→B→C的方向向C运动．当其中一个点到达终点时，另一个也随之停止．设运动时间为t秒．
    （1）当t为何值时，PB与AQ互相平分？
    （2）设△PAQ的面积为S，求S与t的函数关系式．当t为何值时，S有最大值？最大值是多少？
    （3）在整个运动过程中，是否存在某一时刻t，使得以PQ为直径的圆与y轴相切？若存在，求出相应的t值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2014年中考数学二轮精品复习动点型问题练习卷（解析版） 题型：解答题

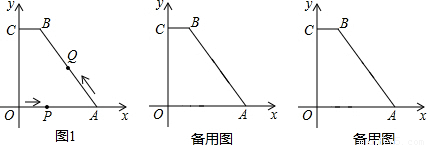
    如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．


    （1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
    （2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（贵州遵义卷）数学（解析版） 题型：解答题

    如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．

    （1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？

    （2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．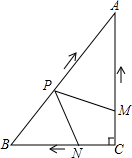

    （1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
    （2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

    查看答案和解析>>


    同步练习册答案