
科目:初中数学 来源: 题型:
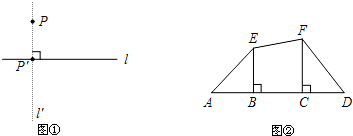
科目:初中数学 来源: 题型:解答题
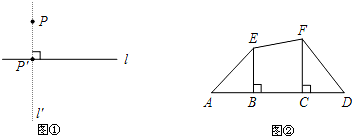
科目:初中数学 来源:2009年江苏省南京市白下区中考数学一模试卷(解析版) 题型:解答题
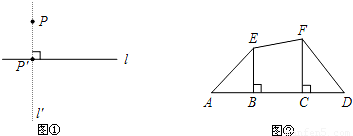
科目:初中数学 来源:北京市燕山区2010年初中毕业考试数学试卷 题型:044
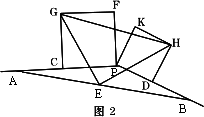
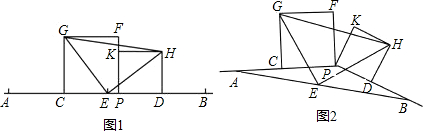
已知:图1,点P在线段AB上(AP>PB),C、D、E分别是AP、PB、AB的中点,正方形CPFG和正方形PDHK在直线AB同侧.
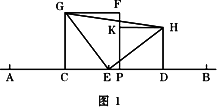
(1)求证:△EHG是等腰直角三角形;
(2)若将图1中的射线PB连同正方形PDHK绕点P顺时针旋转一个角度后,其它已知条件不变,图2,判断△EHG还是等腰直角三角形吗?请说明理由.
科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com