
科目:初中数学 来源:不详 题型:单选题
A. | B. | C. | D. |

科目:初中数学 来源: 题型:阅读理解
| A.好举里巷谐媟以为抚掌之资抚掌:拍手,表示高兴。 |
| B.经营粉本,高下浓淡经营:经度营造 |
| C.不事雕饰,雅合自然雅:文雅 |
| D.尺寸勿爽爽:差错 |
| A.尽其心力以求仿佛赵王岂以一璧之故欺秦邪 |
| B.则李工部之横云之二虫,又何知 |
| C.辄数见焉吴之民方痛心焉 |
| D.与人交,好谈人之善始可与言《诗》已矣 |
| A.本文所记述的张南垣尤擅长垒石造山,具有山水画的意境,构思巧妙,师法自然。 |
| B.本文例举了张南垣所建造园林的代表作及其建造过程,说明他的建造风格,并指出他的技艺符合园林建造的规律。 |
| C.本文还描写了张南垣的外貌性格,因为生得黑而矮胖,又喜欢拿街头巷尾荒唐不经的传说作为谈笑的资料,所以他自己也常常被人调笑耍弄,但他从不与人计较。 |
| D.全文语言流畅工丽,结构严谨,写人状物,如在目前。 |
科目:初中数学 来源: 题型:
| 编号 | 材料 | 长度(m) | 横截面积 (mm2) |
| A | 镍铬合 | 0.3 | 0.5 |
| B | 镍铬合金 | 0.6 | 0.5 |
| C | 镍铬合金 | 0.3 | 1.0 |
| D | 康铜丝 | 0.3 | 0.5 |
| E | 康铜丝 | 0.3 | 1.0 |
| F | 康铜丝 | 0.8 | 0.8 |
科目:初中数学 来源:2012年初中毕业升学考试(内蒙古赤峰卷)数学(带解析) 题型:解答题
阅读材料:
(1)对于任意两个数 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当 时,一定有
时,一定有 ;
;
当 时,一定有
时,一定有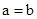 ;
;
当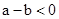 时,一定有
时,一定有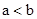 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数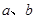 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵ ,
,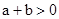
∴( )与(
)与(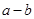 )的符号相同
)的符号相同
当 >0时,
>0时,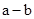 >0,得
>0,得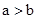
当 =0时,
=0时,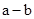 =0,得
=0,得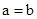
当 <0时,
<0时,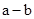 <0,得
<0,得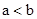
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
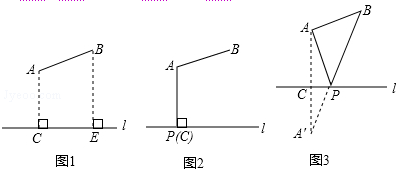
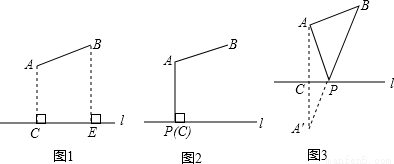
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
科目:初中数学 来源:2012年初中毕业升学考试(内蒙古赤峰卷)数学(解析版) 题型:解答题
阅读材料:
(1)对于任意两个数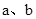 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当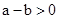 时,一定有
时,一定有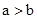 ;
;
当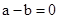 时,一定有
时,一定有 ;
;
当 时,一定有
时,一定有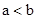 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数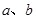 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵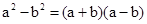 ,
,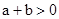
∴(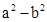 )与(
)与(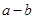 )的符号相同
)的符号相同
当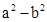 >0时,
>0时,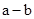 >0,得
>0,得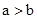
当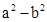 =0时,
=0时,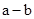 =0,得
=0,得
当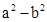 <0时,
<0时,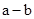 <0,得
<0,得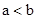
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
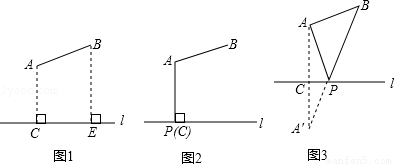
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
科目:初中数学 来源:内蒙古自治区中考真题 题型:解答题
 阅读材料:(1)对于任意两个数
阅读材料:(1)对于任意两个数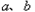 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当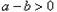 时,一定有
时,一定有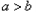 ;当
;当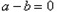 时,一定有
时,一定有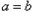 ;当
;当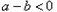 时,一
时,一 定有
定有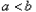 .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.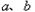 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: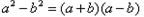 ,
,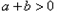
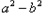 )与(
)与(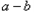 )的符号相同
)的符号相同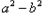 >0时,
>0时,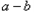 >0,得
>0,得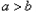
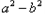 =0时,
=0时,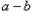 =0,得
=0,得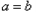
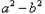 <0时,
<0时,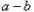 <0,得
<0,得
科目:初中数学 来源:2012年内蒙古赤峰市中考数学试卷(解析版) 题型:解答题
科目:初中数学 来源: 题型:阅读理解
| x2+48 |
| x2+48 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com