
科目:初中数学 来源: 题型:
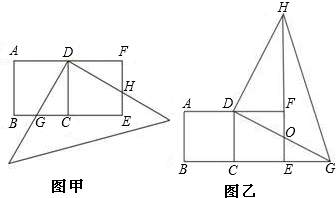
2
| ||
| 3 |
科目:初中数学 来源: 题型:
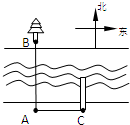 26、如图,七年级(6)班的小毛站在河边的A点处,观察河对面(正北方向)点B处的一棵小树,他很想知道自己距离这棵树有多远.可是身边没有测量的工具,于是他运用本学期学到的数学知识,设计了如下方案:
26、如图,七年级(6)班的小毛站在河边的A点处,观察河对面(正北方向)点B处的一棵小树,他很想知道自己距离这棵树有多远.可是身边没有测量的工具,于是他运用本学期学到的数学知识,设计了如下方案:科目:初中数学 来源: 题型:解答题
 ,结果保留一位小数)
,结果保留一位小数)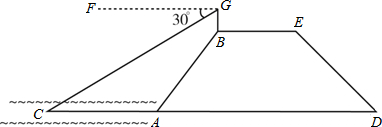
科目:初中数学 来源: 题型:解答题
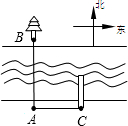 、小树B与自己现在所处的位置E在同一条直线上时,小毛向正南方向恰好走了40步.
、小树B与自己现在所处的位置E在同一条直线上时,小毛向正南方向恰好走了40步.科目:初中数学 来源: 题型:解答题
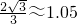 ).
).
科目:初中数学 来源:江苏省期末题 题型:解答题

科目:初中数学 来源:江苏期末题 题型:解答题

科目:初中数学 来源:2012年江苏省盐城市滨海县中考数学二模试卷(解析版) 题型:解答题
 ,结果保留一位小数)
,结果保留一位小数)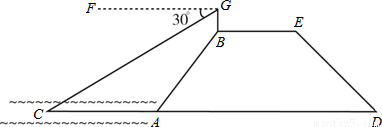
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com