
科目:初中数学 来源: 题型:
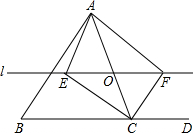 如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.
如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.
如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.科目:初中数学 来源: 题型:044
如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O作直线 ∥BC,直线
∥BC,直线 与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.
与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.
(1)OE与OF相等吗?为什么?
(2)探索:当点O在何处时,四边形AECF为矩形?为什么?

科目:初中数学 来源: 题型:
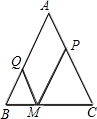 如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.科目:初中数学 来源: 题型:
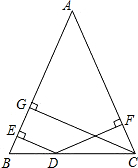 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.科目:初中数学 来源: 题型:
| BP | PC |
科目:初中数学 来源: 题型:
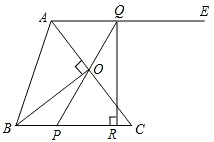 确的共有( )
确的共有( )| 14 |
| 5 |
| A、2条 | B、3条 | C、4条 | D、5条 |
科目:初中数学 来源: 题型:
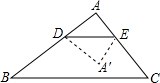 在四边形DBCE所在的平面内),所得的△A'DE与梯形DBCE重叠部分的面积记为y.
在四边形DBCE所在的平面内),所得的△A'DE与梯形DBCE重叠部分的面积记为y.科目:初中数学 来源: 题型:
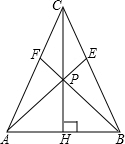 与BC,AC交于点E,F.
与BC,AC交于点E,F.科目:初中数学 来源: 题型:
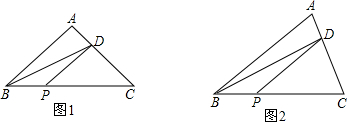
 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.
如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com