
科目:高中数学 来源:2012-2013学年内蒙古鄂尔多斯市达拉特旗十一中高一(上)期末数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
科目:高中数学 来源: 题型:解答题
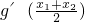 >0;
>0; λx3-
λx3- λ2x2-2λ3x+1在(m,+∞)内为“勾函数”?若存在,试求出m的取值范围,若不存在,说明理由.
λ2x2-2λ3x+1在(m,+∞)内为“勾函数”?若存在,试求出m的取值范围,若不存在,说明理由.科目:高中数学 来源: 题型:解答题
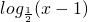 是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;科目:高中数学 来源:2012年上海市浦东新区高考预测数学试卷(文科)(解析版) 题型:解答题
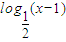 是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com