下列四个函数中是R上的减函数的为( )| A.y=()-x | B.y=log22-x | C.y= | D.y=x2 |
|
相关习题
科目:高中数学
来源:2009-2010学年广东省中山市龙山中学高一(上)第二次段考数学试卷(解析版)
题型:选择题
下列四个函数中是R上的减函数的为( )
A.

B.

C.

D.y=x
2
查看答案和解析>>
科目:高中数学
来源:
题型:
下列四个函数中是R上的减函数的为( )
| | | |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列四个函数中是R上的减函数的为( )
| A.y=()-x | B.y=log22-x | C.y= | D.y=x2 |
查看答案和解析>>
科目:高中数学
来源:
题型:
已知下列四个命题:
①命题“已知f(x)是R上的减函数,若a+b≥0,则f(a)+f(b)≤f(-a)+f(-b)”的逆否命题为真命题;
②若p或q为真命题,则p、q均为真命题;
③若命题p:?x∈R,x
2-x+1<0,则?p:?x∈R,x
2-x+1≥0;
④“
sinx=”是“
x=”的充分不必要条件.
其中正确的是( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省舟山市嵊泗中学高三(上)第一次月考数学试卷(解析版)
题型:填空题
给出下列四个命题:
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<a<1,则函数f(x)=x
2+a
x-3只有一个零点;
③函数

在

上是单调递减函数;
④若lga+lgb=lg(a+b),则a+b的最小值为4.
其中真命题的序号是
(把所有真命题的序号都填上).
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖北省宜昌一中高三(上)12月月考数学试卷(文科)(解析版)
题型:填空题
给出下列四个结论:
①函数y=a
x(a>0且a≠1)与函数y=log
aa
x(a>0且a≠1)的定义域相同;
②函数

是奇函数;
③函数y=sin(-2x)在区间

上是减函数;
④函数y=cos|x|是周期函数;
⑤对于命题p:?x∈R,使得x
2+x+1<0,则¬p:?x∈R,均有x
2+x+1≥0.(其中“?”表示“存在”,“?”表示“任意”).
其中错误结论的序号是
.(填写你认为错误的所有结论序号)
查看答案和解析>>
科目:高中数学
来源:2012年山东省日照市高考数学一模试卷(理科)(解析版)
题型:解答题
给出下列四个命题:
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<a<1,则函数f(x)=x
2+a
x-3只有一个零点;
③函数

在

上是单调递减函数;
④若lga+lgb=lg(a+b),则a+b的最小值为4.
其中真命题的序号是
(把所有真命题的序号都填上).
查看答案和解析>>
科目:高中数学
来源:2011年山西省高三考前适应性训练数学试卷(理科)(解析版)
题型:选择题
已知下列四个命题:
①命题“已知f(x)是R上的减函数,若a+b≥0,则f(a)+f(b)≤f(-a)+f(-b)”的逆否命题为真命题;
②若p或q为真命题,则p、q均为真命题;
③若命题p:?x∈R,x
2-x+1<0,则¬p:?x∈R,x
2-x+1≥0;
④“

”是“

”的充分不必要条件.
其中正确的是( )
A.①④
B.②③
C.①③
D.②④
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
给出下列四个结论:
①函数y=ax(a>0且a≠1)与函数y=logaax(a>0且a≠1)的定义域相同;
②函数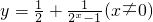 是奇函数;
是奇函数;
③函数y=sin(-2x)在区间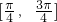 上是减函数;
上是减函数;
④函数y=cos|x|是周期函数;
⑤对于命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,均有x2+x+1≥0.(其中“?”表示“存在”,“?”表示“任意”).
其中错误结论的序号是________.(填写你认为错误的所有结论序号)
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
给出下列四个命题:
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<a<1,则函数f(x)=x2+ax-3只有一个零点;
③函数 在
在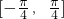 上是单调递减函数;
上是单调递减函数;
④若lga+lgb=lg(a+b),则a+b的最小值为4.
其中真命题的序号是________(把所有真命题的序号都填上).
查看答案和解析>>




 在
在 上是单调递减函数;
上是单调递减函数; 是奇函数;
是奇函数; 上是减函数;
上是减函数; 在
在 上是单调递减函数;
上是单调递减函数; ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件.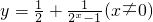 是奇函数;
是奇函数;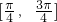 上是减函数;
上是减函数; 在
在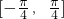 上是单调递减函数;
上是单调递减函数;