
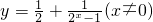 是奇函数;
是奇函数; 上是减函数;
上是减函数;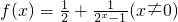 ,可以证明得
,可以证明得 =-f(x),故原函数是奇函数;对于③,函数y=sin(-2x)=-sin(2x)在区间
=-f(x),故原函数是奇函数;对于③,函数y=sin(-2x)=-sin(2x)在区间 上是增函数,命题错误;对于④,由于余弦函数是偶函数,故函数y=cos|x|=cosx,函数是周期函数最小正同期为2π,命题正确;对于⑤,这是一个含有量词的命题,否定时要先改下量词,再否定结论,由此可得命题⑤正确.说明只有③是错误的.
上是增函数,命题错误;对于④,由于余弦函数是偶函数,故函数y=cos|x|=cosx,函数是周期函数最小正同期为2π,命题正确;对于⑤,这是一个含有量词的命题,否定时要先改下量词,再否定结论,由此可得命题⑤正确.说明只有③是错误的.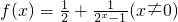 ,
,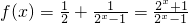 ,
, =-f(x),故原函数是奇函数;
=-f(x),故原函数是奇函数; 上是增函数,命题错误;
上是增函数,命题错误;

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 3x-1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com