
已知F(x)=mf(x)+ng(x)+x+2对任意x∈(0,+∞)都有F(x)≤F(2)=8,且f(x)与g(x)都是奇函数,则在(-∞,0)上F(x)有( )
|
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:单选题
| A.最大值8 | B.最小值-8 | C.最大值-10 | D.最小值-4 |
科目:高中数学 来源:2012-2013学年福建省龙岩一中高一(上)期中数学试卷(解析版) 题型:选择题
科目:高中数学 来源:2010-2011学年黑龙江省大庆市铁人中学高三(上)第二次月考数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源: 题型:填空题
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
科目:高中数学 来源: 题型:
已知f(x)、g(x)都是定义在R上的函数,如果存在实数m,n使得h(x)=mf(x)+ng(x),那么称h(x)为f(x)、g(x)在R上生成的一个函数,设f(x)=x2+ax,g(x)=x+b,(a,b∈R),r(x)=2x2+3x-1,h(x)为f(x)、g(x)在R上生成的一个二次函数。
(1)设a=1,b=2,若h(x)为偶函数,求h(![]() );
);
(2)设b>0,若h(x)同时也是g(x)、r(x)在R上生成的一个函数,求a+b的最小值;
(3)试判断h(x)能否为任意一个二次函数,并证明你的结论。
科目:高中数学 来源: 题型:解答题
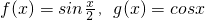 .
. ,且G(x)的最大值为
,且G(x)的最大值为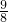 ,求G(x)的解析式.
,求G(x)的解析式.科目:高中数学 来源:2009-2010学年河北省衡水中学高一(上)三调数学试卷(解析版) 题型:解答题
 .
. ,且G(x)的最大值为
,且G(x)的最大值为 ,求G(x)的解析式.
,求G(x)的解析式.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com