练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在数列（an）中，an=2n-1，若一个7行12列的矩阵的第i行第j列的元素cij=ai?aj+ai+aj（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（　　）
    A．18B．28C．48D．63
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：上海 题型：单选题

    在数列（an）中，an=2n-1，若一个7行12列的矩阵的第i行第j列的元素cij=ai•aj+ai+aj（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（　　）
    A．18B．28C．48D．63

    查看答案和解析>>

    科目：高中数学 来源：2013年上海市高考数学试卷（理科）（解析版） 题型：选择题

    在数列（an）中，an=2n-1，若一个7行12列的矩阵的第i行第j列的元素cij=ai•aj+ai+aj（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（ ）
    A．18
    B．28
    C．48
    D．63

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•上海）在数列（an）中，an=2n-1，若一个7行12列的矩阵的第i行第j列的元素cij=ai•aj+ai+aj（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a2=p（p是不等于0的常数），Sn为数列{an}的前n项和，若对任意的正整数n都有Sn=
    n(an-a1)
    2
    ．
    （1）证明：数列{an}为等差数列；
    （2）记bn=
    Sn+2
    Sn+1
    +
    Sn+1
    Sn+2
    ，求数列{bn}的前n项和Tn；
    （3）记cn=Tn-2n，是否存在正整数N，使得当n＞N时，恒有cn∈（
    5
    2
    ，3），若存在，请证明你的结论，并给出一个具体的N值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知数列{an}中，a2=p（p是不等于0的常数），Sn为数列{an}的前n项和，若对任意的正整数n都有Sn=数学公式．
    （1）证明：数列{an}为等差数列；
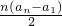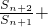
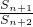    （2）记bn=数学公式数学公式，求数列{bn}的前n项和Tn；
    （3）记cn=Tn-2n，是否存在正整数N，使得当n＞N时，恒有cn∈（数学公式，3），若存在，请证明你的结论，并给出一个具体的N值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012年吉林省高考数学仿真模拟试卷9（理科）（解析版） 题型：解答题

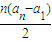    已知数列{an}中，a2=p（p是不等于0的常数），Sn为数列{an}的前n项和，若对任意的正整数n都有Sn=．
    （1）证明：数列{an}为等差数列；
    （2）记bn=，求数列{bn}的前n项和Tn；
    （3）记cn=Tn-2n，是否存在正整数N，使得当n＞N时，恒有cn∈（，3），若存在，请证明你的结论，并给出一个具体的N值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年高考数学总复习备考综合模拟试卷（3）（解析版） 题型：解答题

    已知数列{an}中，a2=p（p是不等于0的常数），Sn为数列{an}的前n项和，若对任意的正整数n都有Sn=．
    （1）证明：数列{an}为等差数列；
    （2）记bn=，求数列{bn}的前n项和Tn；
    （3）记cn=Tn-2n，是否存在正整数N，使得当n＞N时，恒有cn∈（，3），若存在，请证明你的结论，并给出一个具体的N值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}满足an=2an-1+2n-1（n≥2），其中a3=25．若存在一个实数λ，使得{
    an+λ2n
    }    为等差数列，则λ=
    -1
    -1
    ．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年浙江省温州二中高三（上）期中数学试卷（理科）（解析版） 题型：填空题

    数列{an}满足an=2an-1+2n-1（n≥2），其中a3=25．若存在一个实数λ，使得为等差数列，则λ=    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    数列{an}满足an=2an-1+2n-1（n≥2），其中a3=25．若存在一个实数λ，使得数学公式为等差数列，则λ=________．

    查看答案和解析>>


    同步练习册答案