练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
    关于函数f(x)=(2x)*
    1
    2x
    的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为奇函数；③函数f（x）的单调递增区间为(-∞，-
    1
    2
    )，(
    1
    2
    ，+∞)    ．其中所有正确说法的个数为（　　）
    A．0B．1C．2D．3
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
    关于函数f(x)=(2x)*
    1
    2x
    的性质，有如下说法：
    ①函数f（x）的最小值为3；
    ②函数f（x）为奇函数；
    ③函数f（x）的单调递增区间为(-∞，-
    1
    2
    )，(
    1
    2
    ，+∞)    ．
    其中所有正确说法的个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在实数集R中定义一种运算“*”，对任意为唯一确定的实数，且具有性质：

       （1）对任意    （2）对任意

       （3）对任意

           关于函数的性质，有如下说法：①函数的最小值为3；②函数为奇函数；③函数的单调递增区间为。其中所有正确说法的个数为                           （    ）

           A．0      B．1       C．2       D．3

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三下学期数学单元测试5-文科 题型：选择题

     在实数集R中定义一种运算“*”，对任意为唯一确定的实数，且具有性质：

       （1）对任意 

       （2）对任意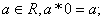

       （3）对任意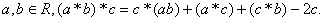

    关于函数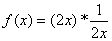的性质，有如下说法：①函数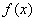的最小值为3；②函数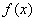为奇函数；③函数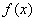的单调递增区间为。其中所有正确说法的个数为                   （    ）

        A．0    B．1    C．2    D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三下学期数学单元测试5-理科 题型：选择题

     在实数集R中定义一种运算“*”，对任意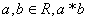为唯一确定的实数，且具有性质：

       （1）对任意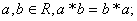   （2）对任意

       （3）对任意

        关于函数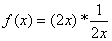的性质，有如下说法：①函数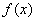的最小值为3；②函数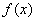为奇函数；③函数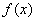的单调递增区间为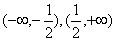。其中所有正确说法的个数为               （    ）

        A．0    B．1    C．2    D．3

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在实数集R中定义一种运算“”，对任意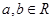,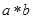为唯一确定的实数，且具有性质：
    （1）对任意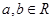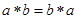， （2）对任意的，；
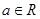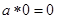    （4）对任意，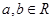
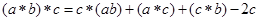
    关于函数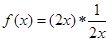的性质，有如下说法：
    1函数f(x)的最小值为3  2函数f(x)为奇函数 3函数f(x)的单调递增区间为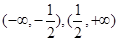，其中所有正确说法的个数(   )

    A．0 B．1 C．2 D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在实数集R中定义一种运算“⊕”，对任意a，b∈R，a⊕b为唯一确定的实数且具有性质：
    （1）对任意a，b∈R，有a⊕b=b⊕a；
    （2）对任意a∈R，有a⊕0=a；
    （3）对任意a，b，c∈R，有（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（c⊕b）-2c．
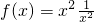    已知函数数学公式，则下列命题中：
    （1）函数f（x）的最小值为3；
    （2）函数f（x）为奇函数；
    （3）函数f（x）的单调递增区间为（-1，0）、（1，+∞）．
    其中正确例题的序号有________．

    查看答案和解析>>

    科目：高中数学 来源：枣庄一模 题型：单选题

    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
    关于函数f(x)=(2x)*
    1
    2x
    的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为奇函数；③函数f（x）的单调递增区间为(-∞，-
    1
    2
    )，(
    1
    2
    ，+∞)    ．其中所有正确说法的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省莆田四中高三（上）第二次月考数学试卷（理科）（解析版） 题型：选择题

    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
    关于函数的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为奇函数；③函数f（x）的单调递增区间为．其中所有正确说法的个数为（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：2009年山东省枣庄市高考数学一模试卷（理科）（解析版） 题型：选择题

    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
    关于函数的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为奇函数；③函数f（x）的单调递增区间为．其中所有正确说法的个数为（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省名校高三数学一轮复习综合测试（五）（解析版） 题型：选择题

    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
    （1）对任意a，b∈R，a*b=b*a；
    （2）对任意a∈R，a*0=a；
    （3）对任意a，b∈R，（a*b）*c=c*（ab）+（a*c）+（c*b）-2c．
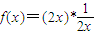    关于函数的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为奇函数；③函数f（x）的单调递增区间为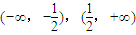．其中所有正确说法的个数为（ ）
    A．0
    B．1
    C．2
    D．3

    查看答案和解析>>


    同步练习册答案