
若函数f(x)=sinωx+acosωx(ω>0)的图象关于点M(
|
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
| A、0 | B、3 | C、6 | D、9 |
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
科目:高中数学 来源:不详 题型:单选题
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| A.0 | B.1 | C.2 | D.3 |
科目:高中数学 来源:月考题 题型:单选题
 对称,且满足f(
对称,且满足f( )=f(
)=f( ),则a+ω的一个可能的取值是
),则a+ω的一个可能的取值是 科目:高中数学 来源:河北省月考题 题型:单选题
 对称,且在
对称,且在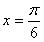 处函数有最小值,则a+ω的一个可能的取值是
处函数有最小值,则a+ω的一个可能的取值是科目:高中数学 来源: 题型:解答题
 (sinωx+acosωx)(a∈R,0<ω≤1)满足:f(x)=f(
(sinωx+acosωx)(a∈R,0<ω≤1)满足:f(x)=f( -x),f(x-π)=f(x+π).
-x),f(x-π)=f(x+π).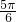 ,
, )内有两个不等的实根”的充分不必要条件.
)内有两个不等的实根”的充分不必要条件.科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| x0 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| a |
| π |
| 6 |
| b |
| π |
| 2 |
| a |
| b |
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| x0 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com