练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：
    ①各侧面和底面所成的二面角相等；
    ②点O到各侧面的距离相等；
    ③侧棱PA=PB=PC=PD；
    ④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．
    其中正确的是（　　）
    A．①②③B．②③④C．①②④D．①③④
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：
    ①各侧面和底面所成的二面角相等；
    ②点O到各侧面的距离相等；
    ③侧棱PA=PB=PC=PD；
    ④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．
    其中正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年黑龙江省鹤岗一中高二（上）期末数学试卷（理科）（解析版） 题型：选择题

    已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：
    ①各侧面和底面所成的二面角相等；
    ②点O到各侧面的距离相等；
    ③侧棱PA=PB=PC=PD；
    ④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．
    其中正确的是（ ）
    A．①②③
    B．②③④
    C．①②④
    D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：
    ①各侧面和底面所成的二面角相等；
    ②点O到各侧面的距离相等；
    ③侧棱PA=PB=PC=PD；
    ④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．
    其中正确的是


    1. A.
      ①②③
    2. B.
      ②③④
    3. C.
      ①②④
    4. D.
      ①③④

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：
    ①各侧面和底面所成的二面角相等；
    ②点O到各侧面的距离相等；
    ③侧棱PA=PB=PC=PD；
    ④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．
    其中正确的是（　　）
    A．①②③ B．②③④ C．①②④ D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AA1=2，底面四边形ABCD的边长均大于2，且∠DAB=45°，点P在底面ABCD内运动且在AB，AD上的射影分别为M，N，若|PA|=2，则三棱锥P-D1MN体积的最大值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AA1=2，底面ABCD的边长均大于2，且∠DAB=45°，点P在底面ABCD内运动且在AB，AD上的射影分别为M，N，若|PA|=2，则三棱锥P-D1MN体积的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知四棱锥S-ABCD的底面是边长为4的正方形，S在底面上的射影O落在正方形ABCD内，SO的长为3，O到AB，AD的距离分别为2和1，P是SC的中点．
    （Ⅰ）求证：平面SOB⊥底面ABCD；
    （Ⅱ）设Q是棱SA上的一点，若
    AQ
    =
    3
    4
    AS
    ，求平面BPQ与底面ABCD所成的锐二面角余弦值的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知四棱锥S—ABCD的底面是边长为4的正方形,S在底面的射影O在正方形ABCD内,且O到AB,AD的距离分别为2和1.

    (1)求证:·是定值;

    (2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•东城区二模）已知四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AA1=2，底面ABCD的边长均大于2，且∠DAB=45°，点P在底面ABCD内运动且在AB，AD上的射影分别为M，N，若|PA|=2，则三棱锥P-D1MN体积的最大值为
    1
    3
    (
    		2
    -1)
    1
    3
    (
    		2
    -1)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

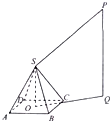    精英家教网房屋的天花板上点P处有一光源，P在地面上的射影为Q，在地面上放置正棱锥S-ABCD，底面ABCD接触地面，已知正四棱锥S-ABCD的高为1米，底面ABCD的边长为
    12
    米，Q与正方形ABCD的中心O的距离为3米，又PQ长为3米，则棱锥影子（不包括底面ABCD）的面积的最大值为
     
    ．（注：正四棱锥为底面是正方形，且顶点在底面的射影是底面的中心的棱锥）

    查看答案和解析>>


    同步练习册答案