
设数列{an}的各项均为正数,前n项和为Sn,对于任意的n∈N+,an,Sn,an2成等差数列,设数列{bn}的前n项和为Tn,且bn=
|
科目:高中数学 来源: 题型:
| lnnx |
| an2 |
科目:高中数学 来源: 题型:解答题
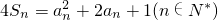 .
.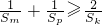 ;
;科目:高中数学 来源: 题型:解答题
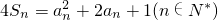
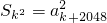 ,若存在,求出k的值;若不存在请说明理由;
,若存在,求出k的值;若不存在请说明理由;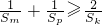 .
.科目:高中数学 来源:闵行区一模 题型:解答题
| a | 2n |
| a | 2k+2048 |
| 1 |
| Sm |
| 1 |
| Sp |
| 2 |
| Sk |
科目:高中数学 来源:不详 题型:单选题
| lnnx |
| an2 |
| A.1 | B.2 | C.3 | D.4 |
科目:高中数学 来源:2012-2013学年山东省济宁市泗水一中高三(上)期末数学模拟试卷(理科)(解析版) 题型:选择题
 成等差数列,设数列{bn}的前n项和为Tn,且
成等差数列,设数列{bn}的前n项和为Tn,且 ,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为( )
,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为( )科目:高中数学 来源:2013年上海市闵行区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
.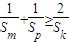 ;
;科目:高中数学 来源:2013年上海市闵行区高考数学一模试卷(文科)(解析版) 题型:解答题
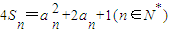
 ,若存在,求出k的值;若不存在请说明理由;
,若存在,求出k的值;若不存在请说明理由; .
.科目:高中数学 来源:四川省绵阳市高中2010届高三二诊(文) 题型:解答题
设数列{an}的各项均为正数,前n项和为Sn,已知 (n∈N*).
(n∈N*).
(1)证明{an}是等差数列,并求an;
(2)设m、k、p∈N*,m+p=2k,求证: +
+ ≥
≥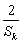 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
科目:高中数学 来源: 题型:单选题
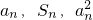 成等差数列,设数列{bn}的前n项和为Tn,且
成等差数列,设数列{bn}的前n项和为Tn,且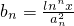 ,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为
,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com