练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若抛物线C以坐标原点为顶点，以双曲线
    y2
    16
    -
    x2
    9
    =1    的顶点为焦点且过第二象限，则抛物线C的准线方程是（　　）
    A．x=3B．y=-4C．x=3或y=-4D．x=4或y=-3
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    若抛物线C以坐标原点为顶点，以双曲线
    y2
    16
    -
    x2
    9
    =1    的顶点为焦点且过第二象限，则抛物线C的准线方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若抛物线C以坐标原点为顶点，以双曲线
    y2
    16
    -
    x2
    9
    =1    的顶点为焦点且过第二象限，则抛物线C的准线方程是（　　）
    A．x=3B．y=-4C．x=3或y=-4D．x=4或y=-3

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年湖南省永州市祁阳县陶铸中学等八校高二（上）联考数学试卷（理科）（解析版） 题型：选择题

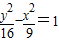    若抛物线C以坐标原点为顶点，以双曲线的顶点为焦点且过第二象限，则抛物线C的准线方程是（ ）
    A．x=3
    B．y=-4
    C．x=3或y=-4
    D．x=4或y=-3

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年湖南省永州市祁阳县陶铸中学等八校高二（上）联考数学试卷（文科）（解析版） 题型：选择题

    若抛物线C以坐标原点为顶点，以双曲线的顶点为焦点且过第二象限，则抛物线C的准线方程是（ ）
    A．x=3
    B．y=-4
    C．x=3或y=-4
    D．x=4或y=-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

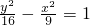    若抛物线C以坐标原点为顶点，以双曲线数学公式的顶点为焦点且过第二象限，则抛物线C的准线方程是


    1. A.
      x=3
    2. B.
      y=-4
    3. C.
      x=3或y=-4
    4. D.
      x=4或y=-3

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：填空题

    已知以坐标原点为顶点的抛物线C，焦点在x轴上，直线x-y=0与抛物线C交于A、B两点．若P(2，2)为AB的中点，则抛物线C的方程为（    ）。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆以坐标原点为中心，坐标轴为对称轴，且椭圆以抛物线y2=16x的焦点为其一个焦点，以双曲线
    x2
    16
    -
    y2
    9
    =1    的焦点为顶点．
    （1）求椭圆的标准方程；
    （2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点P是线段CD上的动点，求
    AP
    •
    BP
    的取值范围．
    （3）试问在圆x2+y2=a2上，是否存在一点M，使△F1MF2的面积S=b2（其中a为椭圆的半长轴长，b为椭圆的半短轴长，F1，F2为椭圆的两个焦点），若存在，求tan∠F1MF2的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年江苏省无锡市部分学校高三4月联考数学试卷（解析版） 题型：解答题

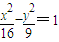    已知椭圆以坐标原点为中心，坐标轴为对称轴，且椭圆以抛物线y2=16x的焦点为其一个焦点，以双曲线的焦点为顶点．
    （1）求椭圆的标准方程；
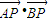    （2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点P是线段CD上的动点，求的取值范围．
    （3）试问在圆x2+y2=a2上，是否存在一点M，使△F1MF2的面积S=b2（其中a为椭圆的半长轴长，b为椭圆的半短轴长，F1，F2为椭圆的两个焦点），若存在，求tan∠F1MF2的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：高考数学最后冲刺必读题解析30讲（25）（解析版） 题型：解答题

    已知椭圆以坐标原点为中心，坐标轴为对称轴，且椭圆以抛物线y2=16x的焦点为其一个焦点，以双曲线的焦点为顶点．
    （1）求椭圆的标准方程；
    （2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点P是线段CD上的动点，求的取值范围．
    （3）试问在圆x2+y2=a2上，是否存在一点M，使△F1MF2的面积S=b2（其中a为椭圆的半长轴长，b为椭圆的半短轴长，F1，F2为椭圆的两个焦点），若存在，求tan∠F1MF2的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知曲线C为顶点在原点，以x轴为对称轴，开口向右的抛物线，又点M（2，1）到抛物线C的准线的距离为，

    （1）求抛物线C的方程；

    （2）证明：过点M的任意一条直线与抛物线恒有公共点；

    （3）若（2）中的直线（i=1，2，3， 4）分别与抛物线C交于上下两点，又点的纵坐标依次成公差不为0的等差数列，试分析的大小关系。

    查看答案和解析>>


    同步练习册答案