
科目:高中数学 来源:2008-2009学年浙江省绍兴一中高二(上)期末数学试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源:2008-2009学年浙江省绍兴一中高二(上)期末数学试卷(理科)(解析版) 题型:选择题
科目:高中数学 来源:2014届四川省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
已知抛物线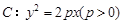 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设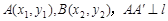 于
于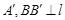 于
于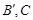 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②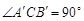 ;
;
③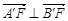 ; ④
; ④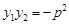 ; ⑤.
; ⑤.
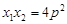
其中一定正确的有 (写出所有正确结论的序号).
科目:高中数学 来源: 题型:填空题
已知抛物线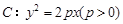 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设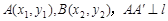 于
于 于
于 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ② ;
;
③ ; ④
; ④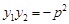 ; ⑤.
; ⑤. 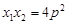
其中一定正确的有 (写出所有正确结论的序号).
科目:高中数学 来源:不详 题型:填空题
 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设 于
于 于
于 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ② ;
;  ; ④
; ④ ; ⑤.
; ⑤. 
科目:高中数学 来源: 题型:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com