
若曲线y=f(x)在点(x0,f(x0))处的切线方程为y=2x-1,则( )
|
科目:高中数学 来源:不详 题型:单选题
| A.f′(x0)=0 | B.f′(x0)>0 | C.f′(x0)<0 | D.f′(x0)不存在 |
科目:高中数学 来源:不详 题型:单选题
| A.f′(x0)>0 | B.f′(x0)=0 | C.f′(x0)<0 | D.f′(x0)不存在 |
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:2013届浙江省、兰溪一中高二下期中理科数学试卷(解析版) 题型:解答题
(1)已知函数f(x)=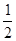 x
x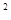 -ax+(a-1)
-ax+(a-1)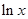 ,
,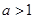 。讨论函数
。讨论函数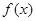 的单调性;
的单调性;
(2).已知函数f (x)=lnx,g(x)=ex.设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.问在区间(1,+∞)上是否存在x0,使得直线l与曲线y=g(x)也相切.若存在,这样的x0有几个?,若没有,则说明理由。
科目:高中数学 来源:不详 题型:解答题
 x
x -ax+(a-1)
-ax+(a-1) ,
, 。讨论函数
。讨论函数 的单调性;
的单调性; 科目:高中数学 来源: 题型:
科目:高中数学 来源:天津月考题 题型:解答题
 .
.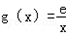 ,若在[1,e]上至少存在一点x0,使得
,若在[1,e]上至少存在一点x0,使得科目:高中数学 来源:汕头二模 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com