
已知不等边三角形的两边长分别是2cm和9cm,如果第三边的长为整数,那么第三边的长为( )
|
科目:初中数学 来源:南岗区二模 题型:单选题
| A.8cm | B.10cm | C.8cm或10cm | D.8cm或9cm |
科目:初中数学 来源:2011年黑龙江省哈尔滨市南岗区中考数学二模试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
| 3 |
| ||
| 2 |
| 3 |
| 2 |
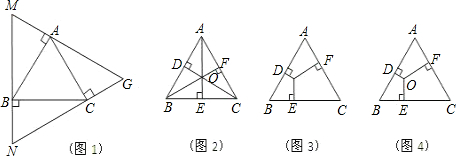
科目:初中数学 来源: 题型:解答题
 a;
a; a;结论2. AD+BE+CF=
a;结论2. AD+BE+CF= a;
a;
科目:初中数学 来源: 题型:
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
①如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.![]() ;结论2.
;结论2.![]() ;
;
②如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
科目:初中数学 来源: 题型:
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
(2)如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):
① 结论1.![]() ;
;
② 结论2.![]() ;
;
(3)如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
科目:初中数学 来源: 题型:
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
①如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.![]() ;结论2.
;结论2.![]() ;
;
②如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com