
科目:初中数学 来源:第4章《视图与投影》易错题集(31):4.1 视图(解析版) 题型:选择题
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源: 题型:
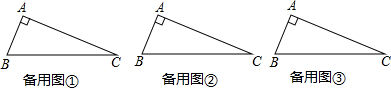
小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?
(1)①请你帮小明在图2的画板内画出你的测量方案(简要说明画法过程);
②说出该画法的依据的定理.
(2)小明在此基础上![]() 又进行了更深入的探究,想到两个操作:
又进行了更深入的探究,想到两个操作:
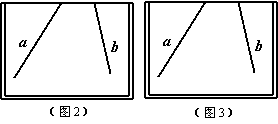
①在图3的画板内,在直线a和b上各取一点,使这两点与直线a、b的交点构成等腰三角形(其中交点为顶角的顶点),画出该等腰三角形在画板内的部分;
②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)在图3的画板内,作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.请你帮小明完成上面两个操作过程.
 (必须要有方案图,所有的线不能画到画板外,只能画在画板内).
(必须要有方案图,所有的线不能画到画板外,只能画在画板内).
 |
科目:初中数学 来源: 题型:
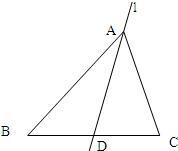 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是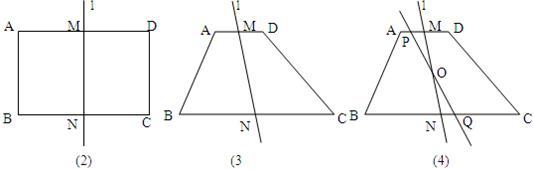
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com