
已知直线y=x上有两点A(1,1),B(3,3),在y轴上存在一点P,它到点A,B的距离之和最小,则点P的纵坐标是( )
|
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| A、4 | B、6 | C、7 | D、8 |
科目:初中数学 来源: 题型:
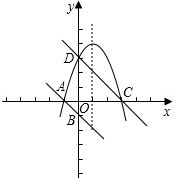 y轴交于C、D两点.
y轴交于C、D两点.科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
 直线y=
直线y=| 1 |
| 2 |
科目:初中数学 来源: 题型:
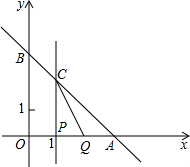 A上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图).
A上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图).科目:初中数学 来源: 题型:解答题
 y轴交于C、D两点.
y轴交于C、D两点.科目:初中数学 来源: 题型:解答题
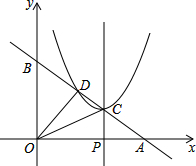 已知直线y=-
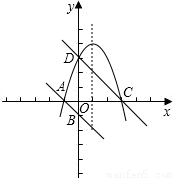
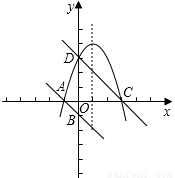
已知直线y=- x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设运动时间为t秒.
x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设运动时间为t秒.科目:初中数学 来源:2013届浙江省桐乡三中九年级上学期期中考试数学试卷(带解析) 题型:单选题
已知直线l外的两点A、B,且A、B在直线l两旁,则经过A、B两点且圆心在直线l上的圆有( )
A. 0个或1个;
B. 1个或无数个;
C. 0个或无数个;
D. 0个或1个或无数个;
科目:初中数学 来源:第2章《二次函数》中考题集(36):2.3 二次函数的应用(解析版) 题型:解答题
科目:初中数学 来源:第6章《二次函数》中考题集(36):6.4 二次函数的应用(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com