
如果一个平行四边形要成为正方形,需增加的条件是( )
|
科目:初中数学 来源:新课程同步练习 数学 八年级下册 人教版 题型:013
如果一个平行四边形要成为一个正方形,需要增加的条件是
A.对角线互相垂直
B.对角互补
C.对角线互相垂直且相等
D.对角线相等
科目:初中数学 来源:数学教研室 题型:013
A.对角线互相垂直 B.对角互补
C.对角线互相垂直且相等 D.对角线相等
科目:初中数学 来源: 题型:阅读理解
阅读下列材料:
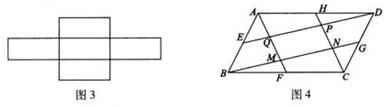
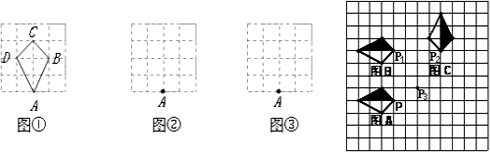
小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB的中点O旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG.

请你参考小明的做法解决下列问题:
(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形.要求:在图3中画出并 指明拼接成的平行四边形(画出一个符合条件的平行四边形即可);
(2)如图4,在面积为2的平行四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,分别连结AF、BG、CH、DE得到一个新的平行四边形MNPQ请在图4中探究平行四边形MNPQ面积的大小(画图并直接写出结果).
科目:初中数学 来源: 题型:
| 2 |
| 5 |
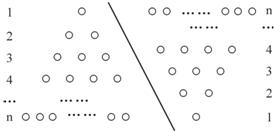
科目:初中数学 来源: 题型:阅读理解
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com