精英家教网 > 高中数学 > 题目详情

圆心在P（-1，2），半径是2的圆的标准方程是（　　）

A．（x-1）²+（y-2）²=2	B．（x+1）²+（y-2）²=4
C．（x-2）²+（y+1）²=4	D．（x-1）²+（y-2）²=4

相关习题

科目：高中数学 来源： 题型：

14、圆心在P（-1，2），半径是2的圆的标准方程是（　　）

A、（x-1）²+（y-2）²=2

B、（x+1）²+（y-2）²=4

C、（x-2）²+（y+1）²=4

D、（x-1）²+（y-2）²=4

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

圆心在P（-1，2），半径是2的圆的标准方程是（　　）

A．（x-1）²+（y-2）²=2	B．（x+1）²+（y-2）²=4
C．（x-2）²+（y+1）²=4	D．（x-1）²+（y-2）²=4

查看答案和解析>>

科目：高中数学 来源：2009-2010学年广东省佛山市高明区高一（上）模块考试数学试卷（必修2）（解析版） 题型：选择题

圆心在P（-1，2），半径是2的圆的标准方程是（）
A．（x-1）²+（y-2）²=2
B．（x+1）²+（y-2）²=4
C．（x-2）²+（y+1）²=4
D．（x-1）²+（y-2）²=4

查看答案和解析>>

科目：高中数学 来源： 题型：单选题

圆心在P（-1，2），半径是2的圆的标准方程是

A.
（x-1）²+（y-2）²=2
B.
（x+1）²+（y-2）²=4
C.
（x-2）²+（y+1）²=4
D.
（x-1）²+（y-2）²=4

查看答案和解析>>

科目：高中数学 来源：0108 模拟题 题型：解答题

（1）已知点C 的极坐标为（2，

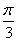），画图并求出以C为圆心，半径r=2的圆的极坐标方程（写出解题过程）；
（2）P是以原点为圆心，r=2的圆上的任意一点，Q（6，0），M是PQ中点
①画图并写出⊙O的参数方程；
②当点P在圆上运动时，求点M的轨迹的参数方程。

查看答案和解析>>

科目：高中数学 来源：2012年江苏省南京市苏州市梁丰高级中学高考数学一模试卷（解析版） 题型：解答题

（1）选修4-2矩阵与变换：
已知矩阵M=

，其中a∈R，若点P（1，-2）在矩阵M的变换下得到点P′（-4，0）．
①求实数a的值；
②求矩阵M的特征值及其对应的特征向量．
（2）选修4-4参数方程与极坐标：
已知曲线C的极坐标方程是ρ=4cosθ．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是

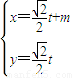（t是参数）．若l与C相交于AB两点，且

．
①求圆的普通方程，并求出圆心与半径；
②求实数m的值．

查看答案和解析>>

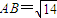科目：高中数学 来源： 题型：

已知半径为2的圆的圆心C在x轴上，圆心C的横坐标是非负整数，且与直线4x+3y+10=0相切．
（Ⅰ）求圆C的方程；
（Ⅱ）设直线l：y=kx+1与圆相交于P、Q两点，若

•

=-2，求k的值；
（Ⅲ）已知直线l：y=kx+1，过点（0，1）作直线l₁与l垂直，且直线l₁与圆C交于M、N两点，求四边形PQMN面积的最大值．

查看答案和解析>>

科目：高中数学 来源：2012-2013学年甘肃省张掖市山丹一中高二（上）期中数学试卷（解析版） 题型：解答题

•

=-2，求k的值；
（Ⅲ）已知直线l：y=kx+1，过点（0，1）作直线l₁与l垂直，且直线l₁与圆C交于M、N两点，求四边形PQMN面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

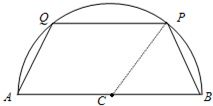如图，半圆形公园上有P和Q两点，线段AB是该半圆的一条直径，C为圆心，半径是2km，现要在公园内建一块顶点都在半圆C上的多边形活动场地为等腰梯形ABPQ．
（1）若设PQ=2x（km），求场地面积S关于x的函数关系式；
（2）若设∠PCB=θ，求场地面积S关于θ的函数关系式；
（3）选择（1）、（2）中的一个函数的关系式，求场地面积S的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y-29=0相切．
（1）求圆的方程；
（2）若直线ax-y+5=0（a≠0）与圆相交于A，B两点，是否存在实数a，使得过点P（-2，4）的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

圆心在P（-1，2），半径是2的圆的标准方程是