某同学在研究函数f(x)=(x∈R)时,给出了下面几个结论:
①函数f(x)的值域为(-1,1);②若f(x1)=f(x2),则恒有x1=x2;③f(x)在(-∞,0)上是减函数;
④若规定f1(x)=f(x),fn+1(x)=f[fn(x)],则fn(x)=对任意n∈N*恒成立,
上述结论中所有正确的结论是( ) |
相关习题
科目:高中数学
来源:
题型:
某同学在研究函数
f(x)=(x∈R)时,给出了下面几个结论:
①函数f(x)的值域为(-1,1);②若f(x
1)=f(x
2),则恒有x
1=x
2;③f(x)在(-∞,0)上是减函数;
④若规定f
1(x)=f(x),f
n+1(x)=f[f
n(x)],则
fn(x)=对任意n∈N*恒成立,
上述结论中所有正确的结论是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
某同学在研究函数
f(x)=(x∈R)时,给出了下面几个结论:
①函数f(x)的值域为(-1,1);②若f(x
1)=f(x
2),则恒有x
1=x
2;③f(x)在(-∞,0)上是减函数;
④若规定f
1(x)=f(x),f
n+1(x)=f[f
n(x)],则
fn(x)=对任意n∈N*恒成立,
上述结论中所有正确的结论是( )
查看答案和解析>>
科目:高中数学
来源:上海模拟
题型:填空题
某同学在研究函数
f(x)= (x∈R)时,分别给出下面几个结论:
①等式f(-x)+f(x)=0对x∈R恒成立;
②若f(x
1)≠f(x
2),则一定有x
1≠x
2;
③若m>0,方程|f(x)|=m有两个不等实数根;
④函数g(x)=f(x)-x在R上有三个零点.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:
题型:
某同学在研究函数
f(x)=(x∈R)时,分别得出如下几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(-2,2);
③若x
1≠x
2,则一定有f(x
1)≠f(x
2);
④函数y(x)=f(x)-2x在R上有三个零点.
其中正确的序号有
①②③
①②③
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省淮北一中高一(上)期中数学试卷(解析版)
题型:填空题
某同学在研究函数 f (x)=

(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x
1≠x
2,则一定有f (x
1)≠f (x
2);
④方程f(x)-x=0有三个实数根.
其中正确结论的序号有
.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省淮北一中高一(上)期中数学试卷(解析版)
题型:填空题
某同学在研究函数 f (x)=

(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x
1≠x
2,则一定有f (x
1)≠f (x
2);
④方程f(x)-x=0有三个实数根.
其中正确结论的序号有
.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省广州市执信中学高一(上)期中数学试卷(解析版)
题型:填空题
某同学在研究函数 f (x)=
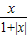
(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x
1≠x
2,则一定有f (x
1)≠f (x
2);
④方程f(x)-x=0有三个实数根.
其中正确结论的序号有
.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:2009-2010学年江苏省镇江市高一(上)期中数学试卷(解析版)
题型:填空题
某同学在研究函数 f (x)=
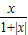
(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x
1≠x
2,则一定有f (x
1)≠f (x
2);
④方程f(x)-x=0有三个实数根.
其中正确结论的序号有
.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:
题型:填空题
某同学在研究函数 f (x)=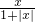 (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x1≠x2,则一定有f (x1)≠f (x2);
④方程f(x)-x=0有三个实数根.
其中正确结论的序号有________.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省绍兴市诸暨中学高一(上)期中数学试卷(解析版)
题型:选择题
某同学在研究函数

(x∈R)时,给出了下面几个结论:
①函数f(x)的值域为(-1,1);②若f(x
1)=f(x
2),则恒有x
1=x
2;③f(x)在(-∞,0)上是减函数;
④若规定f
1(x)=f(x),f
n+1(x)=f[f
n(x)],则

对任意n∈N*恒成立,
上述结论中所有正确的结论是( )
A.②③
B.②④
C.①③
D.①②④
查看答案和解析>>

 (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论: (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论: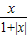 (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论: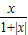 (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论: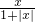 (x∈R) 时,分别给出下面几个结论:
(x∈R) 时,分别给出下面几个结论: (x∈R)时,给出了下面几个结论:
(x∈R)时,给出了下面几个结论: 对任意n∈N*恒成立,
对任意n∈N*恒成立,