
若关于x的一元二次方程ax2+(2a-1)x-2=0 的两根相等,那么a等于( )
|
科目:初中数学 来源:不详 题型:单选题
| A.-0.5 | B.0.5 | C.0.5或-0.5 | D.-0.5或0 |
科目:初中数学 来源:《23.3 实践与探索》2010年水平测试(解析版) 题型:选择题
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
科目:初中数学 来源: 题型:阅读理解
-b+
| ||
| 2a |
-b-
| ||
| 2a |
| b |
| a |
| c |
| a |
| 3 |
| 2 |
 <0<x2,(AO+OB)2=12•OC+1.
<0<x2,(AO+OB)2=12•OC+1.科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 6 |
5+2
|
科目:初中数学 来源: 题型:解答题
 =12+2
=12+2 +(
+( )2=(1+
)2=(1+ )2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:
)2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如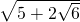 的双重二次根式)
的双重二次根式)科目:初中数学 来源:广东省期中题 题型:解答题
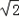 =12+2
=12+2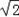 +(
+( )2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:
)2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com