已知Sn是非零数列{an}的前n项和,且Sn=2an-1,则S2011等于( )| A.1-22010 | B.22011-1 | C.22010-1 | D.1-22011 |
|
相关习题
科目:高中数学
来源:
题型:
已知Sn是非零数列{an}的前n项和,且Sn=2an-1,则S2011等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知S
n是非零数列{a
n}的前n项和,且S
n=2a
n-1,则S
2011等于( )
| A.1-22010 | B.22011-1 | C.22010-1 | D.1-22011 |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年河南省焦作市武陟一中高考第一轮复习质量检测标准试卷3(理科)(解析版)
题型:选择题
已知Sn是非零数列{an}的前n项和,且Sn=2an-1,则S2011等于( )
A.1-22010
B.22011-1
C.22010-1
D.1-22011
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知Sn是非零数列{an}的前n项和,且Sn=2an-1,则S2011等于
- A.
1-22010
- B.
22011-1
- C.
22010-1
- D.
1-22011
查看答案和解析>>
科目:高中数学
来源:
题型:
数列{a
n}的前n项和记为S
n,前kn项和记为S
kn(n,k∈N
*),对给定的常数k,若
是与n无关的非零常数t=f(k),则称该数列{a
n}是“k类和科比数列”.
(理科)(1)已知
Sn=()2,an>0,求数列{a
n}的通项公式;
(2)证明(1)的数列{a
n}是一个“k类和科比数列”;
(3)设正数列{c
n}是一个等比数列,首项c
1,公比Q(Q≠1),若数列{lgc
n}是一个“k类和科比数列”,探究c
1与Q的关系.
查看答案和解析>>
科目:高中数学
来源:
题型:
数列{a
n}的前n项和记为S
n,前kn项和记为S
kn(n,k∈N
*),对给定的常数k,若
是与n无关的非零常数t=f(k),则称该数列{a
n}是“k类和科比数列”.
(1)已知
Sn=an-(n∈N*),求数列{a
n}的通项公式;
(2)在(1)的条件下,数列
an=2cn,求证数列c
n是一个“1 类和科比数列”(4分);
(3)设等差数列{b
n}是一个“k类和科比数列”,其中首项b
1,公差D,探究b
1与D的数量关系,并写出相应的常数t=f(k).
查看答案和解析>>
科目:高中数学
来源:2012年江苏省无锡市辅仁高级中学高三3月联考数学试卷(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,前kn项和记为S
kn(n,k∈N
*),对给定的常数k,若

是与n无关的非零常数t=f(k),则称该数列{a
n}是“k类和科比数列”.
(理科)(1)已知

,求数列{a
n}的通项公式;
(2)证明(1)的数列{a
n}是一个“k类和科比数列”;
(3)设正数列{c
n}是一个等比数列,首项c
1,公比Q(Q≠1),若数列{lgc
n}是一个“k类和科比数列”,探究c
1与Q的关系.
查看答案和解析>>
科目:高中数学
来源:2011年上海市奉贤区高考数学一模试卷(文理合卷)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,前kn项和记为S
kn(n,k∈N
*),对给定的常数k,若
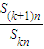
是与n无关的非零常数t=f(k),则称该数列{a
n}是“k类和科比数列”.
(1)已知
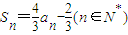
,求数列{a
n}的通项公式;
(2)在(1)的条件下,数列
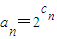
,求证数列c
n是一个“1 类和科比数列”(4分);
(3)设等差数列{b
n}是一个“k类和科比数列”,其中首项b
1,公差D,探究b
1与D的数量关系,并写出相应的常数t=f(k).
查看答案和解析>>
科目:高中数学
来源:2011年上海市奉贤区高考数学一模试卷(文理合卷)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,前kn项和记为S
kn(n,k∈N
*),对给定的常数k,若

是与n无关的非零常数t=f(k),则称该数列{a
n}是“k类和科比数列”.
(理科)(1)已知

,求数列{a
n}的通项公式;
(2)证明(1)的数列{a
n}是一个“k类和科比数列”;
(3)设正数列{c
n}是一个等比数列,首项c
1,公比Q(Q≠1),若数列{lgc
n}是一个“k类和科比数列”,探究c
1与Q的关系.
查看答案和解析>>
科目:高中数学
来源:湖南省保靖县民族中学2011-2012学年高二上学期期中考试数学理科试题
题型:044
已知非零数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(Ⅰ)求数列{an},{bn}的通项an和bn;
(Ⅱ)设cn=an·bn,数列{cn}的前n项和为Tn,若不等式nTn>a·2n+6n对任意的n∈N*恒成立,求实数a的取值范围.
查看答案和解析>>

 是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.
是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”. ,求数列{an}的通项公式;
,求数列{an}的通项公式;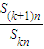 是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.
是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.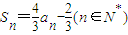 ,求数列{an}的通项公式;
,求数列{an}的通项公式;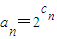 ,求证数列cn是一个“1 类和科比数列”(4分);
,求证数列cn是一个“1 类和科比数列”(4分); 是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.
是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”. ,求数列{an}的通项公式;
,求数列{an}的通项公式;