
已知随机变量ξ的分布列为下图,则ξ最可能出现的值是( )
|
科目:高中数学 来源:2008年浙江省宁波市镇海中学高考冲刺《概率与统计》系列训练1(解析版) 题型:选择题
| -1 | 1 | ||
| P | 0.5 | 0.3 | 0.2 |
科目:高中数学 来源:2013-2014学年湖南省益阳市高三第一次模拟考试理数学试卷(解析版) 题型:选择题
有下列四种说法:
①命题:“ ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”;
②已知随机变量 服从正态分布
服从正态分布 ,
, ,则
,则 ;
;
③函数 图像关于直线
图像关于直线 对称,且在区间
对称,且在区间 上是增函数;
上是增函数;
④设实数 ,则满足:
,则满足: 的概率为
的概率为 。其中错误的个数是 ( )
。其中错误的个数是 ( )
A、0 B、1 C、2 D、3。
科目:高中数学 来源: 题型:单选题
有下列四种说法:
①命题:“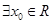 ,使得
,使得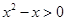 ”的否定是“
”的否定是“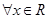 ,都有
,都有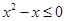 ”;
”;
②已知随机变量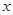 服从正态分布
服从正态分布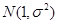 ,
,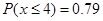 ,则
,则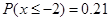 ;
;
③函数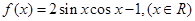 图像关于直线
图像关于直线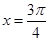 对称,且在区间
对称,且在区间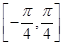 上是增函数;
上是增函数;
④设实数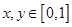 ,则满足:
,则满足: 的概率为
的概率为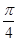 。其中错误的个数是 ( )
。其中错误的个数是 ( )
| A.0 | B.1 | C.2 | D.3。 |
科目:高中数学 来源:不详 题型:单选题
 ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”; 服从正态分布
服从正态分布 ,
, ,则
,则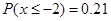 ;
;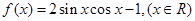 图像关于直线
图像关于直线 对称,且在区间
对称,且在区间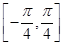 上是增函数;
上是增函数;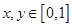 ,则满足:
,则满足: 的概率为
的概率为 。其中错误的个数是 ( )
。其中错误的个数是 ( )| A.0 | B.1 | C.2 | D.3。 |
科目:高中数学 来源: 题型:
| 1 |
| x2 |
| 1 |
| 2 |
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
科目:高中数学 来源: 题型:
| 1 | x |
科目:高中数学 来源:浙江省高考真题 题型:解答题

科目:高中数学 来源:2013届浙江省、兰溪一中高二下期中理科数学试卷(解析版) 题型:解答题
如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,

2,3等奖.(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量 的分布列及期望
的分布列及期望 ;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com