| 函数y=cos2ωx-sin2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+)的一个单调递增区间是( ) |
相关习题
科目:高中数学
来源:海珠区二模
题型:单选题
函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+
)的一个单调递增区间是( )
查看答案和解析>>
科目:高中数学
来源:2009年广东省广州市海珠区高考数学二模试卷(理科)(解析版)
题型:选择题
函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+

)的一个单调递增区间是( )
A.[-

,

]
B.[-

,

]
C.[-

,

]
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2009年广东省广州市海珠区高考数学二模试卷(文科)(解析版)
题型:选择题
函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+

)的一个单调递增区间是( )
A.[-

,

]
B.[-

,

]
C.[-

,

]
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2011年上海市黄浦区大同中学高考数学专项训练:三角函数(解析版)
题型:选择题
函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+

)的一个单调递增区间是( )
A.[-

,
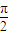
]
B.[-
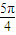
,

]
C.[-

,

]
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2010年11月上海市大同中学高三数学练习试卷(三角专项)(解析版)
题型:选择题
函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+

)的一个单调递增区间是( )
A.[-

,

]
B.[-

,

]
C.[-

,

]
D.[
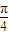
,
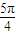
]
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
函数y=cos2ωx-sin2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+ )的一个单调递增区间是
)的一个单调递增区间是
- A.
[-
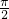
,
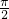
]
- B.
[-
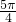
,
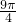
]
- C.
[-

,
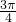
]
- D.
[

,
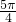
]
查看答案和解析>>
科目:高中数学
来源:
题型:
(2009•海珠区二模)函数y=cos
2ωx-sin
2ωx(ω>0)的最小正周期是π,则函数f(x)=2sin(ωx+
)的一个单调递增区间是( )
查看答案和解析>>
科目:高中数学
来源:2010-2011学年广东省广州市育才中学高三(上)各类题型综合训练:三角函数(解析版)
题型:解答题
已知向量

=(

,2),
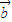
=(sin2ωx,-cos
2ωx),(ω>0).
(1)若
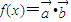
,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合;
(2)在(1)的条件下,f(x)沿向量

平移可得到函数y=2sin2x,求向量

.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知向量
=(
,2),
=(sin2ωx,-cos
2ωx),(ω>0).
(1)若
f(x)=•,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合;
(2)在(1)的条件下,f(x)沿向量
平移可得到函数y=2sin2x,求向量
.
查看答案和解析>>

 )的一个单调递增区间是( )
)的一个单调递增区间是( ) ,
, ]
] ,
, ]
] ,
, ]
] ,
, ]
] )的一个单调递增区间是( )
)的一个单调递增区间是( ) ,
, ]
] ,
, ]
] ,
, ]
] ,
, ]
] )的一个单调递增区间是( )
)的一个单调递增区间是( ) ,
,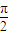 ]
]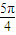 ,
, ]
] ,
, ]
] ,
, ]
] )的一个单调递增区间是( )
)的一个单调递增区间是( ) ,
, ]
] ,
, ]
] ,
, ]
]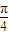 ,
,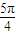 ]
] )的一个单调递增区间是
)的一个单调递增区间是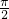 ,
,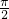 ]
]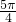 ,
,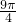 ]
] ,
,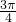 ]
] ,
,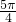 ]
] =(
=( ,2),
,2), =(sin2ωx,-cos2ωx),(ω>0).
=(sin2ωx,-cos2ωx),(ω>0).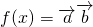 ,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合;
,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合; 平移可得到函数y=2sin2x,求向量
平移可得到函数y=2sin2x,求向量 .
. =(
=( ,2),
,2),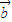 =(sin2ωx,-cos2ωx),(ω>0).
=(sin2ωx,-cos2ωx),(ω>0).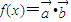 ,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合;
,且f(x)的最小正周期为π,求f(x)的最大值,并求f(x)取得最大值时x的集合; 平移可得到函数y=2sin2x,求向量
平移可得到函数y=2sin2x,求向量 .
.