
若线段a:b=c:d,则下列结论中正确的是( )
|
科目:初中数学 来源: 题型:
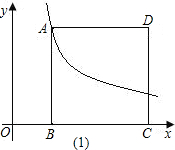
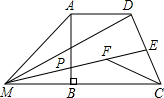 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°-
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°-| 1 |
| 2 |
| A、①②④ | B、①③④ |
| C、②③ | D、①②③④ |
科目:初中数学 来源: 题型:
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:| 1 |
| 2 |
科目:初中数学 来源:2013年甘肃省兰州市中考数学模拟试卷(三)(解析版) 题型:选择题
 ∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是( )
∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是( )
科目:初中数学 来源:2012年4月份中考数学模拟试卷(九)(解析版) 题型:选择题
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论: ∠FCM;③△ABM∽△CEF; ④S梯形AMCD-2S△EFC=3S△MFC,正确的是( )
∠FCM;③△ABM∽△CEF; ④S梯形AMCD-2S△EFC=3S△MFC,正确的是( )科目:初中数学 来源:2012年浙江省金华市义乌市中考数学模拟试卷(一)(解析版) 题型:选择题
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论: ∠FCM;③△ABM∽△CEF; ④S梯形AMCD-2S△EFC=3S△MFC,正确的是( )
∠FCM;③△ABM∽△CEF; ④S梯形AMCD-2S△EFC=3S△MFC,正确的是( )科目:初中数学 来源:2011年湖北省武汉六中中考数学模拟试卷(3月份)(解析版) 题型:选择题
 ∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是( )
∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是( )
科目:初中数学 来源: 题型:解答题
 上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0).
上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0).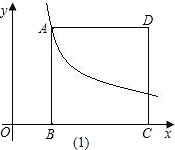
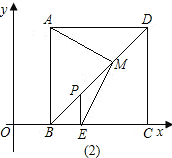
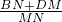 值不变;
值不变;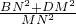 的值不变.其中有且仅有一个是正确的,请选择正确的结论证明并求其值.
的值不变.其中有且仅有一个是正确的,请选择正确的结论证明并求其值.
科目:初中数学 来源: 题型:
| 2 |
| x |
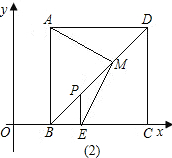
| BN+DM |
| MN |
| BN2+DM2 |
| MN2 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com