
Rt△ABC中,∠C=90°,AC=6,BC=8,则Rt△ABC的外接圆半径为( )
|
科目:初中数学 来源: 题型:
| A、点D在⊙C上 | B、点D在⊙C外 | C、点D在⊙C内 | D、无法确定 |
科目:初中数学 来源: 题型:
| A、D在⊙C上 | B、D在⊙C外 | C、D在⊙C内 | D、不能判断 |
科目:初中数学 来源: 题型:
RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠![]() .
.
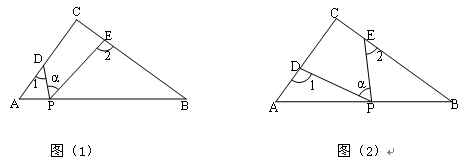
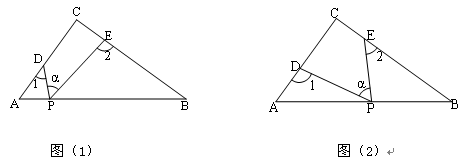
(1)若点P在线段AB上,如图(1)所示,且∠![]() =50°,则∠1+∠2= °;
=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示, 则∠![]() 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠![]() 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。
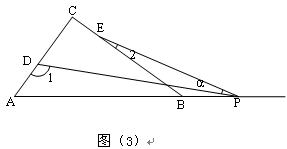
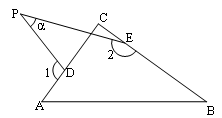
(4)若点P运动到ΔABC形外,如图(4)所示,则∠![]() 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
科目:初中数学 来源: 题型:
 .
.
 =50°,则∠1+∠2= °;
=50°,则∠1+∠2= °;  、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为: 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。
 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
科目:初中数学 来源:2011-2012学年江苏省无锡玉祁初级中学七年级下学期期中考试数学卷(带解析) 题型:解答题
RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠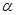 .
.
(1)若点P在线段AB上,如图(1)所示,且∠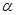 =50°,则∠1+∠2= °;
=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示, 则∠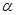 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠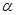 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。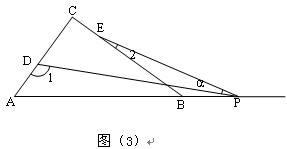
(4)若点P运动到ΔABC形外,如图(4)所示,则∠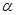 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
科目:初中数学 来源:2014届江苏省七年级下学期期中考试数学卷(解析版) 题型:解答题
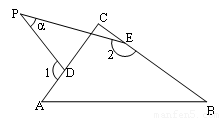
RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠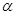 .
.

(1)若点P在线段AB上,如图(1)所示,且∠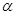 =50°,则∠1+∠2=
°;
=50°,则∠1+∠2=
°;
(2)若点P在边AB上运动,如图(2)所示, 则∠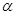 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠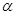 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。

(4)若点P运动到ΔABC形外,如图(4)所示,则∠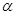 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com