| 设数列{an}满足a1=1，且对任意的n∈N*，点Pn（n，an）都有=(1，2)，则数列{an}的通项公式为（ ） |
相关习题
科目：高中数学
来源：
题型：
设数列{a
n}满足a
1=1，且对任意的n∈N
*，点P
n（n，a
n）都有
=(1，2)，则数列{a
n}的通项公式为（ ）
查看答案和解析>>
科目：高中数学
来源：不详
题型：单选题
设数列{a
n}满足a
1=1，且对任意的n∈N
*，点P
n（n，a
n）都有
=(1，2)，则数列{a
n}的通项公式为（ ）
查看答案和解析>>
科目：高中数学
来源：2009-2010学年浙江省温州市省一级重点中学（八校联考）高一（下）期末数学试卷（解析版）
题型：选择题
设数列{a
n}满足a
1=1，且对任意的n∈N
*，点P
n（n，a
n）都有
，则数列{a
n}的通项公式为（ ）
A．2n-1
B．n
C．2n+1
D．2
n-1
查看答案和解析>>
科目：高中数学
来源：
题型：单选题
设数列{an}满足a1=1，且对任意的n∈N*，点Pn（n，an）都有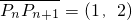
，则数列{an}的通项公式为
- A.
2n-1
- B.
n
- C.
2n+1
- D.
2n-1
查看答案和解析>>
科目：高中数学
来源：
题型：
设数列{a
n}满足a
1=1，a
2=2，a
n=
（a
n-1+2a
n-2）（n=3，4，…）．数列{b
n}满足b
1=1，b
n（n=2，3，…）是非零整数，且对任意的正整数m和自然数k，都有-1≤b
m+b
m+1+…+b
m+k≤1．
（1）求数列{a
n}和{b
n}的通项公式；
（2）记c
n=na
nb
n（n=1，2，…），求数列{c
n}的前n项和S
n．
查看答案和解析>>
科目：高中数学
来源：
题型：
设数列{a
n}满足a
1=1，a
2+a
4=6，且对任意n∈N
*，函数f（x）=（a
n-a
n+1+a
n+2）x+a
n+1?cosx-a
n+2sinx满足
f′()=0若
cn=an+，则数列{c
n}的前n项和S
n为（ ）
查看答案和解析>>
科目：高中数学
来源：广东
题型：解答题
设数列{a
n}满足a
1=1，a
2=2，a
n=
（a
n-1+2a
n-2）（n=3，4，…）．数列{b
n}满足b
1=1，b
n（n=2，3，…）是非零整数，且对任意的正整数m和自然数k，都有-1≤b
m+b
m+1+…+b
m+k≤1．
（1）求数列{a
n}和{b
n}的通项公式；
（2）记c
n=na
nb
n（n=1，2，…），求数列{c
n}的前n项和S
n．
查看答案和解析>>
科目：高中数学
来源：广东省高考真题
题型：解答题
设数列{a
n}满足a
1=1，a
2=2，a
n=
（a
n-1+2a
n-2）（n=3，4，…）。数列{b
n}满足b
1=1，b
n（n=2，3，…）是非零整数，且对任意的正整数m和自然数k，都有-1≤b
m+b
m+1+…+b
m+k≤1，
（1）求数列{a
n}和{b
n}的通项公式；
（2）记c
n=na
nb
n（n=1，2，…），求数列{c
n}的前n项和S
n．
查看答案和解析>>
科目：高中数学
来源：2008年广东省高考数学试卷（文科）（解析版）
题型：解答题
设数列{a
n}满足a
1=1，a
2=2，a
n=
（a
n-1+2a
n-2）（n=3，4，…）．数列{b
n}满足b
1=1，b
n（n=2，3，…）是非零整数，且对任意的正整数m和自然数k，都有-1≤b
m+b
m+1+…+b
m+k≤1．
（1）求数列{a
n}和{b
n}的通项公式；
（2）记c
n=na
nb
n（n=1，2，…），求数列{c
n}的前n项和S
n．
查看答案和解析>>
科目：高中数学
来源：广东省高考数学一轮复习：6.7 数列的求和（解析版）
题型：解答题
设数列{a
n}满足a
1=1，a
2=2，a
n=
（a
n-1+2a
n-2）（n=3，4，…）．数列{b
n}满足b
1=1，b
n（n=2，3，…）是非零整数，且对任意的正整数m和自然数k，都有-1≤b
m+b
m+1+…+b
m+k≤1．
（1）求数列{a
n}和{b
n}的通项公式；
（2）记c
n=na
nb
n（n=1，2，…），求数列{c
n}的前n项和S
n．
查看答案和解析>>
