
现有数列{an}满足:a1=1,且对任意的m,n∈N*都有:am+n=am+an+mn,则
|
科目:高中数学 来源:不详 题型:单选题
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2012 |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:2012-2013学年四川省成都七中高一(下)期中数学试卷(解析版) 题型:选择题
 =( )
=( )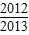
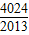
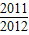
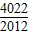
科目:高中数学 来源:模拟题 题型:解答题
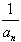 ,不难发现,当a取不同的值时,可以得到不同的数列,例如,当a=1时,得到无穷数列:1,2,
,不难发现,当a取不同的值时,可以得到不同的数列,例如,当a=1时,得到无穷数列:1,2,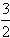 ,
, ,…;当a=-
,…;当a=-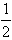 时,得到有穷数列:-
时,得到有穷数列:-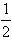 ,-1,0。
,-1,0。 (n∈N*)求证:a取数列{bn}中的任何一个数,都可得到一个有穷数列{an};
(n∈N*)求证:a取数列{bn}中的任何一个数,都可得到一个有穷数列{an}; <an<2成立,试求a 的取值范围。
<an<2成立,试求a 的取值范围。科目:高中数学 来源:浙江省模拟题 题型:填空题
 成立,则称函数f(x)为该区间上的上凸函数. 类比上述定义,对于数列{an},如果对任意正整数n,总有不等式
成立,则称函数f(x)为该区间上的上凸函数. 类比上述定义,对于数列{an},如果对任意正整数n,总有不等式 :成立,则称数列{an}为上凸数列,现有数列{an}满足如下两个条件:
:成立,则称数列{an}为上凸数列,现有数列{an}满足如下两个条件:科目:高中数学 来源: 题型:解答题
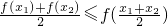 成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式:
成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式: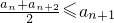 成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:
成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:科目:高中数学 来源:2010年江苏省宿迁中学高考数学模拟试卷(解析版) 题型:填空题
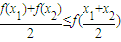 成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式:
成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式: 成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:
成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:科目:高中数学 来源:2010年江苏省南通市如东县掘港中学高考数学一模试卷(解析版) 题型:填空题
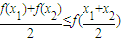 成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式:
成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式: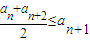 成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:
成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:科目:高中数学 来源:2012年浙江省高考数学冲刺试卷3(理科)(解析版) 题型:解答题
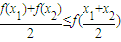 成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式:
成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式: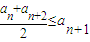 成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:
成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:科目:高中数学 来源:2010年上海市浦东新区高考数学二模试卷(理科)(解析版) 题型:解答题
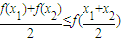 成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式:
成立,则称函数f(x)为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式: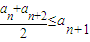 成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:
成立,则称数列{an}为向上凸数列(简称上凸数列).现有数列{an}满足如下两个条件:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com