| 定义:F(x,y)=yx(x>0,y>0),已知数列{an}满足:an=(n∈N*),若对任意正整数n,都有an≤ak(k∈N*)成立,则ak的值为( ) |
相关习题
科目:高中数学
来源:
题型:
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=
(n∈N
*),若对任意正整数n,都有a
n≥a
k(k∈N
*)成立,则a
k的值为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
定义:F(x,y)=y
x(x>0,y>0)
(1)解关于x的不等式F(1,x
2)+F(2,x)≤3x-1;
(2)记f(x)=3•F(1,x),设
Sn=f()+f()+f()+…+f(),若不等式
<对n∈N*恒成立,求实数a的取值范围;
(3)记g(x)=F(x,2),正项数列a
n满足:
a1=3,g(an+1)=8an,求数列a
n的通项公式,并求所有可能的乘积a
i•a
j(1≤i≤j≤n)的和.
查看答案和解析>>
科目:高中数学
来源:
题型:
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=
(n∈N
*),若对任意正整数n,都有a
n≤a
k(k∈N
*)成立,则a
k的值为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
定义:F(x,y)=y
x(x>0,y>0),设数列{a
n}满足a
n=
,若S
n为数列{
}的前n项和,则下列说法正确的是( )
查看答案和解析>>
科目:高中数学
来源:2010-2011学年上海市十校高三(下)第二次联考数学试卷(理科)(解析版)
题型:解答题
定义:F(x,y)=y
x(x>0,y>0)
(1)解关于x的不等式F(1,x
2)+F(2,x)≤3x-1;
(2)记f(x)=3•F(1,x),设
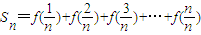
,若不等式
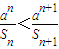
对n∈N*恒成立,求实数a的取值范围;
(3)记g(x)=F(x,2),正项数列a
n满足:
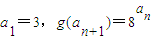
,求数列a
n的通项公式,并求所有可能的乘积a
i•a
j(1≤i≤j≤n)的和.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义:F(x,y)=y
x(x>0,y>0),设数列{a
n}满足a
n=
,若S
n为数列{
}的前n项和,则下列说法正确的是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=
(n∈N
*),若对任意正整数n,都有a
n≤a
k(k∈N
*)成立,则a
k的值为( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年黑龙江省哈师大附中高三(上)第三次月考数学试卷(理科)(解析版)
题型:填空题
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=

(n∈N
*),若对任意正整数n,都有a
n≥a
k(k∈N
*)成立,则a
k的值为
.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年广东省深圳市高级中学高三(上)第一次月考数学试卷(理科)(解析版)
题型:填空题
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=

(n∈N
*),若对任意正整数n,都有a
n≥a
k(k∈N
*)成立,则a
k的值为
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省金华市东阳中学高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
定义:F(x,y)=y
x(x>0,y>0),已知数列{a
n}满足:a
n=

(n∈N
*),若对任意正整数n,都有a
n≤a
k(k∈N
*)成立,则a
k的值为( )
A.

B.2
C.

D.

查看答案和解析>>

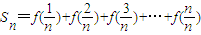 ,若不等式
,若不等式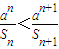 对n∈N*恒成立,求实数a的取值范围;
对n∈N*恒成立,求实数a的取值范围;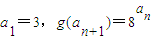 ,求数列an的通项公式,并求所有可能的乘积ai•aj(1≤i≤j≤n)的和.
,求数列an的通项公式,并求所有可能的乘积ai•aj(1≤i≤j≤n)的和. (n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为 .
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为 . (n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为 .
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为 . (n∈N*),若对任意正整数n,都有an≤ak(k∈N*)成立,则ak的值为( )
(n∈N*),若对任意正整数n,都有an≤ak(k∈N*)成立,则ak的值为( )

