
求数的方根,可以用估算的方法,但是这样求方根速度太慢,计算器可以帮你解决这一问题,使你的计算快速大大加快,为此,熟练掌握用计算器求平方根和立方根的程序是关键.在计算器上,按程序2nd?x2?625)enter计算,显示的结果是( )
|
科目:初中数学 来源: 题型:
科目:初中数学 来源:不详 题型:单选题
| A.25 | B.±25 | C.-25 | D.15 |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源:《28.4 方程的近似解》2010年习题精选(解析版) 题型:解答题
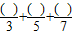 ≈1.16,那么你能算出他们的分子依次是哪些数吗?
≈1.16,那么你能算出他们的分子依次是哪些数吗?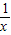 ,用3+
,用3+ 代替x,得x=3+
代替x,得x=3+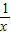 =3+
=3+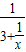 .反复若干次用3+
.反复若干次用3+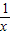 代替x,就得到x=
代替x,就得到x=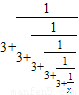 形如上式右边的式子称为连分数.
形如上式右边的式子称为连分数.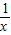 对整个式子的值的影响将越来越小,因此可以根据需要,在适当时候把
对整个式子的值的影响将越来越小,因此可以根据需要,在适当时候把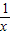 忽略不计,例如,当忽略x=3+
忽略不计,例如,当忽略x=3+ 中的
中的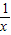 时,就得到x=3;当忽略x=3+
时,就得到x=3;当忽略x=3+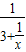 中的
中的 时,就得到x=3+
时,就得到x=3+ ;如此等等,于是可以得到一系列分数;
;如此等等,于是可以得到一系列分数; ,3+
,3+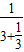 ,3+
,3+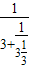 ,…,即3,
,…,即3,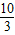 =3.333…,
=3.333…,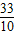 ≈3.3.
≈3.3.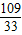 =3.303 03…,….
=3.303 03…,….科目:初中数学 来源: 题型:
| 我们在认识无理数时,有这样一个问题:边长为a的正方形面积是2,那么a2=2,a是有理数吗?我们用“两边夹”的方法,来估算的a取值范围,我们还可以用“逼近”的方法,求出它的近似值. 例如:1.42=1.96,1.52=2.25,在数轴上1.96比2.25更靠近2,当近似值保留一位小数时,a的近似值为1.4. 根据下表给出的数据,当近似值保留两位小数时,a的近似值为( )
|
科目:初中数学 来源:不详 题型:单选题
| x | 1.40 | 1.41 | 1.42 | 1.43 | … |
| x2 | 1.9600 | 1.9881 | 2.0164 | 2.0449 | … |
| A.1.40 | B.1.41 | C.1.42 | D.1.43 |
科目:初中数学 来源: 题型:单选题
| x | 1.40 | 1.41 | 1.42 | 1.43 | … |
| x2 | 1.9600 | 1.9881 | 2.0164 | 2.0449 | … |
科目:初中数学 来源: 题型:
| ( ) |
| 3 |
| ( ) |
| 5 |
| ( ) |
| 7 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 | ||||||||
3+
|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 | ||
3+
|
| 1 | ||||
3+
|
| 10 |
| 3 |
| 33 |
| 10 |
| 109 |
| 33 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com