练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2+3nx+bn=0的两根，则b1+b2+b3+…+b20的和为（　　）
    A．6385B．5836C．3658D．8365
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2-bnx+(
    1
    3
    )n=0    的两根，则b2010=
    2×(
    1
    3
    )1005
    2×(
    1
    3
    )1005
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2+3nx+bn=0的两根，则b1+b2+b3+…+b20的和为（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2+3nx+bn=0的两根，则b1+b2+b3+…+b20的和为（　　）
    A．6385B．5836C．3658D．8365

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    数列{an}满足：a1=1，且对每个n∈N*，an，an+1是方程x2+3nx+bn=0的两根，则b1+b2+b3+…+b20的和为


    1. A.
      6385
    2. B.
      5836
    3. C.
      3658
    4. D.
      8365

    查看答案和解析>>

    科目：高中数学 来源：江西省高考真题 题型：解答题

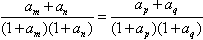    各项均为正数的数列{an}，a1=a，a2=b，且对满足m+n=p+q的正整数m，n，p，q都有。
    （1）当时，求通项an；
    （2）证明：对任意a，存在与a有关的常数λ，使得对于每个正整数n，都有。

    查看答案和解析>>

    科目：高中数学 来源：2009年江西省高考数学试卷（理科）（解析版） 题型：解答题

    各项均为正数的数列{an}，a1=a，a2=b，且对满足m+n=p+q的正整数m，n，p，q都有．
    （1）当时，求通项an；
    （2）证明：对任意a，存在与a有关的常数λ，使得对于每个正整数n，都有．

    查看答案和解析>>

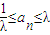    科目：高中数学 来源： 题型：

    可以证明，对任意的n∈N*，有（1+2+…+n）2=13+23+…+n3成立．下面尝试推广该命题：
    （1）设由三项组成的数列a1，a2，a3每项均非零，且对任意的n∈{1，2，3}有（a1+a2+…+an）2=a13+a23+…+an3成立，求所有满足条件的数列；
    （2）设数列{an}每项均非零，且对任意的n∈N*有（a1+a2+…+an）2=a13+a23+…+an3成立，数列{an}的前n项和为Sn．求证：an+12-an+1=2Sn，n∈N*；
    （3）是否存在满足（2）中条件的无穷数列{an}，使得a2011=2009？若存在，写出一个这样的无穷数列（不需要证明它满足条件）； 若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    可以证明，对任意的n∈N*，有（1+2+…+n）2=13+23+…+n3成立．下面尝试推广该命题：
    （1）设由三项组成的数列a1，a2，a3每项均非零，且对任意的n∈{1，2，3}有（a1+a2+…+an）2=a13+a23+…+an3成立，求所有满足条件的数列；
    （2）设数列{an}每项均非零，且对任意的n∈N*有（a1+a2+…+an）2=a13+a23+…+an3成立，数列{an}的前n项和为Sn．求证：an+12-an+1=2Sn，n∈N*；
    （3）是否存在满足（2）中条件的无穷数列{an}，使得a2011=2009？若存在，写出一个这样的无穷数列（不需要证明它满足条件）； 若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省泰州市姜堰市蒋垛中学高三联考数学试卷（解析版） 题型：解答题

    可以证明，对任意的n∈N*，有（1+2+…+n）2=13+23+…+n3成立．下面尝试推广该命题：
    （1）设由三项组成的数列a1，a2，a3每项均非零，且对任意的n∈{1，2，3}有（a1+a2+…+an）2=a13+a23+…+an3成立，求所有满足条件的数列；
    （2）设数列{an}每项均非零，且对任意的n∈N*有（a1+a2+…+an）2=a13+a23+…+an3成立，数列{an}的前n项和为Sn．求证：an+12-an+1=2Sn，n∈N*；
    （3）是否存在满足（2）中条件的无穷数列{an}，使得a2012=-2011？若存在，写出一个这样的无穷数列（不需要证明它满足条件）； 若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•蓟县二模）已知数列{an}的首项a1=1，a2=3，前n项和为Sn，且
    Sn+1-Sn
    Sn-Sn-1
    =
    2an+1
    an
    ，（n∈N*，n≥2），数列{bn}满足b1=1，bn+1=log2（an+1）+bn．
    （Ⅰ）判断数列{an+1}是否为等比数列，并证明你的结论；
    （Ⅱ）设cn=-an(bn-
    n2
    2
    -1)    ，求c1+c2+c3+…+cn；
    （Ⅲ）对于（Ⅰ）中数列{an}，若数列{ln}满足ln=log2（an+1）（n∈N*），在每两个lk与lk+1之间都插入2k-1（k=1，2，3，…k∈N*）个2，使得数列{ln}变成了一个新的数列{tp}，（p∈N*）试问：是否存在正整数m，使得数列{tp}的前m项的和Tm=2011？如果存在，求出m的值；如果不存在，说明理由．

    查看答案和解析>>


    同步练习册答案