练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    设P是关于x的5次多项式，Q是关于x的3次多项式，则（　　）
    A．P+Q是关于x的8次多项式
    B．P-Q是关于x的二次多项式
    C．3P+Q是关于x的8次多项式
    D．P-Q是关于x的五次多项式
    D
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：单选题

    设P是关于x的5次多项式，Q是关于x的3次多项式，则下列说法正确的是


    1. A.
      P+Q是关于x的8次多项式
    2. B.
      P-Q是关于x的2次多项式
    3. C.
      P·Q是关于x的5次多项式
    4. D.
      P·Q是关于x的8次多项式

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    设P是关于x的5次多项式，Q是关于x的3次多项式，则


    1. A.
      P+Q是关于x的8次多项式
    2. B.
      P-Q是关于x的二次多项式
    3. C.
      3P+Q是关于x的8次多项式
    4. D.
      P-Q是关于x的五次多项式

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    设p（x）是一个关于x的二次多项式，且7x3-5x2+6x-m-1=（x-1）p（x）+a，其中m，a是与x无关的常数，则p（x）的表达式是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    7、设P是关于x的5次多项式，Q是关于x的3次多项式，则（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    设P是关于x的5次多项式，Q是关于x的3次多项式，则（　　）
    A．P+Q是关于x的8次多项式
    B．P-Q是关于x的二次多项式
    C．3P+Q是关于x的8次多项式
    D．P-Q是关于x的五次多项式

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下面材料：
    若设关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根为x1，x2，那么由根与系数的关系得：x1+x2=-
    b
    a
    ，x1x2=
    c
    a
    ．∵
    b
    a
    =-(x1+x2)
    c
    a
    =x1x2    ，∴ax2+bx+c=a(x2+
    b
    a
    x+
    c
    a
    )    =a[x2-（x1+x2）x+x1x2]=a（x-x1）（x-x2）．于是，二次三项式就可以分解因式ax2+bx+c=a（x-x1）（x-x2）．
    （1）请用上面的方法将多项式4x2+8x-1分解因式．
    （2）判断二次三项式2x2-4x+7在实数范围内是否能利用上面的方法因式分解，并说明理由．
    （3）如果关于x的二次三项式mx2-2（m+1）x+（m+1）（1-m）能用上面的方法分解因式，试求出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    阅读下面材料：
    若设关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根为x1，x2，那么由根与系数的关系得：x1+x2=-
    b
    a
    ，x1x2=
    c
    a
    ．∵
    b
    a
    =-(x1+x2)
    c
    a
    =x1x2    ，∴ax2+bx+c=a(x2+
    b
    a
    x+
    c
    a
    )    =a[x2-（x1+x2）x+x1x2]=a（x-x1）（x-x2）．于是，二次三项式就可以分解因式ax2+bx+c=a（x-x1）（x-x2）．
    （1）请用上面的方法将多项式4x2+8x-1分解因式．
    （2）判断二次三项式2x2-4x+7在实数范围内是否能利用上面的方法因式分解，并说明理由．
    （3）如果关于x的二次三项式mx2-2（m+1）x+（m+1）（1-m）能用上面的方法分解因式，试求出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：四川省月考题 题型：解答题

    阅读下面材料：若设关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根为x1，x2，
    那么由根与系数的关系得：x1+x2=﹣，x1x2=．
    ∴，
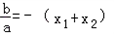
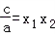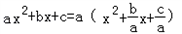    ∴=a[x2﹣（x1+x2）x+x1x2]=a（x﹣x1）（x﹣x2）．
    于是，二次三项式就可以分解因式ax2+bx+c=a（x﹣x1）（x﹣x2）．
    （1）请用上面的方法将多项式4x2+8x﹣1分解因式．
    （2）判断二次三项式2x2﹣4x+7在实数范围内是否能利用上面的方法因式分解，并说明理由．
    （3）如果关于x的二次三项式mx2﹣2（m+1）x+（m+1）（1﹣m）能用上面的方法分解因式，试求出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    为了强化司机的交通安全意识，我市利用交通安全宣传月对司机进行了交通安全知识问卷调查．关于酒驾设计了如下调查问卷：
    　　　　　　　　　　　　　　　　　　　　　　克服酒驾--你认为哪种方式最好？
    A加大宣传力度，增强司机的守法意识． B在汽车上张贴温馨提示：“请勿酒驾”．
    C司机上岗前签“拒接酒驾”保证书．　D加大检查力度，严厉打击酒驾．
    E查出酒驾追究一同就餐人的连带责任．
    随机抽取部分问卷，整理并制作了如下统计图：

    根据上述信息，解答下列问题：
    （1）本次调查的样本容量是多少？
    （2）补全条形图，并计算B选项所对应扇形圆心角的度数；
    （3）若我市有3000名司机参与本次活动，则支持D选项的司机大约有多少人？

    查看答案和解析>>

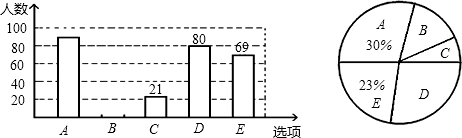
    科目：初中数学 来源： 题型：解答题

    （1）设（x-3）2+|y+1|=0，求代数式x+y的值；
    （2）设a为最小的正整数，b是最大的负整数，c是绝对值最小的数，d是倒数等于本身的有理数，则a+b+c+d=？
    （3）已知A=4x2-4xy+y2，B=x2+xy-5y2，求A-B；
    （4）（3x2y-2xy2）-（xy2-2x2y），其中x=-1，y=2；
    （5）多项式（a-2）x+（2b+1）xy+y3-7是关于x，y的多项式，若该多项式不含二次项和一次项，求3a+2b的值．

    查看答案和解析>>


    同步练习册答案