
科目:初中数学 来源:2007年初中毕业升学考试(江苏南京卷)数学(带解析) 题型:解答题
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点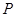 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点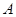 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为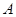 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形 的三边
的三边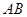 ,
,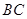 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
科目:初中数学 来源:2007年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.

科目:初中数学 来源:不详 题型:解答题
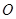 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为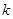 ,并且原多边形上的任一点
,并且原多边形上的任一点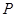 ,它的对应点
,它的对应点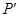 在线段
在线段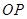 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点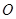 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度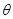 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为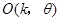 ,其中点
,其中点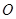 叫做旋转相似中心,
叫做旋转相似中心,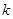 叫做相似比,
叫做相似比,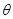 叫做旋转角.
叫做旋转角.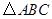 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转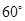 ,得到
,得到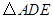 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );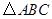 是边长为
是边长为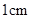 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到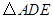 ,则线段
,则线段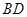 的长为
的长为  ;
;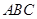 的三边
的三边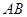 ,
,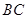 ,
,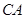 为边向外作正方形
为边向外作正方形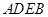 ,
,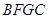 ,
,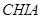 ,点
,点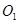 ,
,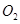 ,
,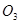 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用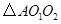 与
与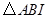 ,
,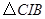 与
与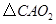 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段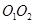 与
与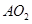 之间的关系.
之间的关系.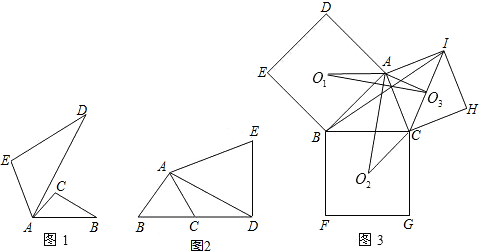
科目:初中数学 来源: 题型:
在平面内,先将一个多边形以点![]() 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为![]() ,并且原多边形上的任一点
,并且原多边形上的任一点![]() ,它的对应点
,它的对应点![]() 在线段
在线段![]() 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点![]() 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度![]() ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为![]() ,其中点
,其中点![]() 叫做旋转相似中心,
叫做旋转相似中心,![]() 叫做相似比,
叫做相似比,![]() 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将![]() 以点
以点![]() 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转![]() ,得到
,得到![]() ,这个旋转相似变换记为
,这个旋转相似变换记为![]() ( , );
( , );
②如图2,![]() 是边长为
是边长为![]() 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换![]() ,得到
,得到![]() ,则线段
,则线段![]() 的长为
的长为 ![]() ;
;
(2)如图3,分别以锐角三角形![]() 的三边
的三边![]() ,
,![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用![]() 与
与![]() ,
,![]() 与
与![]() 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段![]() 与
与![]() 之间的关系.
之间的关系.

科目:初中数学 来源:北师大二附中2007~2008学年度第一学期、初三数学 题型:044
在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角.例如:正方形绕着它的对角线的交点旋转90°后能与自身重合(如图),所以正方形是旋转对称图形,它有一个旋转角为90°

(1)判断下列命题的真假(在相应的括号内填上“真”或“假”)
①等腰梯形是旋转对称图形,它有一个旋转角为180°( )
②矩形是旋转对称图形,它有一个旋转角为180°( )
(2)填空:下列图形中,是旋转对称图形,且有一个旋转角为120°的是________(写出所有正确结论的序号):①正三角形;②正方形;③正六边形;④正八边形
(3)写出两个多边形,它们都是旋转对称图形,都有一个旋转角为72°,并且分别满足下列条件:
①是轴对称图形,但不是中心对称图形:__________________(2个).
②既是轴对称图形,又是中心对称图形:__________________(2个).
科目:初中数学 来源:2008连云港市海州实验中学中考数学模拟试题及答案 题型:044
在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角.例如:正方形绕着它的对角线的交点旋转90°后能与自身重合(如图),所以正方形是旋转对称图形,它有一个旋转角为90°.

(1)判断下列命题的真假(在相应的括号内填上“真”或“假”).
①等腰梯形是旋转对称图形,它有一个旋转角为180°.( )
②矩形是旋转对称图形,它有一个旋转角为180°( )
(2)填空:下列图形中,是旋转对称图形,且有一个旋转角为120°的是________(写出所有正确结论的序号):①正三角形;②正方形;③正六边形;④正八边形.
(3)写出两个多边形,它们都是旋转对图形,都有一个旋转角为72°,并且分别满足下列条件
①是轴对称图形,但不是中心对称图形:________
②既是轴对称图形,又是中心对称图形:________
科目:初中数学 来源: 题型:
在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P’ 在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过放缩和旋转的图形变换叫做旋转相似变换,记为O( k, θ ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空:
①如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A( , );
②如图2,△ABC是边长为![]() 的等边三角形,将它作旋转相似变换A(
的等边三角形,将它作旋转相似变换A(![]() ,90°),得到△ADE,则线段BD的长为 cm;
,90°),得到△ADE,则线段BD的长为 cm;
(2)如图3,分别以锐角三角形ABC的三边AB、BC、CA为边向外作正方形ADEB、BFGC、CHIA,点O1、O2、O3分别是这三个正方形的对角线交点,试分别利用△AO1O3与△ABI、△CIB与△CAO2之间的关系,运用旋转相似变换的知识说明线段O1O3与AO2之间的关系.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com