练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设f（n）=2n+1（n∈N），P={1，2，3，4，5}，Q={3，4，5，6，7}，记
    ?
    P
    ={n∈N|f（n）∈P}，
    ?
    Q
    ={n∈N|f（n）∈Q}，则（
    ?
    P
    ∩CN
    ?
    Q
    ）∪（
    ?
    Q
    ∩CN
    ?
    P
    ）=（　　）
    A．{0，3}B．{1，2}C．（3，4，5}D．{1，2，6，7}
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    设f（n）=2n+1（n∈N），P={1，2，3，4，5}，Q={3，4，5，6，7}，记
    ?
    P
    ={n∈N|f（n）∈P}，
    ?
    Q
    ={n∈N|f（n）∈Q}，则（
    ?
    P
    ∩CN
    ?
    Q
    ）∪（
    ?
    Q
    ∩CN
    ?
    P
    ）=（　　）
    A、{0，3}
    B、{1，2}
    C、{3，4，5}
    D、{1，2，6，7}

    查看答案和解析>>

    科目：高中数学 来源：浙江 题型：单选题

    设f（n）=2n+1（n∈N），P={1，2，3，4，5}，Q={3，4，5，6，7}，记
    ?
    P
    ={n∈N|f（n）∈P}，
    ?
    Q
    ={n∈N|f（n）∈Q}，则（
    ?
    P
    ∩CN
    ?
    Q
    ）∪（
    ?
    Q
    ∩CN
    ?
    P
    ）=（　　）
    A．{0，3}B．{1，2}C．（3，4，5}D．{1，2，6，7}

    查看答案和解析>>

    科目：高中数学 来源：2005年浙江省高考数学试卷（理科）（解析版） 题型：选择题

    设f（n）=2n+1（n∈N），P={1，2，3，4，5}，Q={3，4，5，6，7}，记={n∈N|f（n）∈P}，={n∈N|f（n）∈Q}，则（∩CN）∪（∩）=（ ）
    A．{0，3}
    B．{1，2}
    C．（3，4，5}
    D．{1，2，6，7}

    查看答案和解析>>

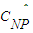    科目：高中数学 来源： 题型：

    设函数f（x）=
    2x
    2x+
    		2
    的图象上两点P1（x1，y1）、P2（x2，y2），若
    OP
    =
    1
    2
    （
    OP1
    +
    OP2
    ），且点P的横坐标为
    1
    2
    ．
    （1）求证：P点的纵坐标为定值，并求出这个定值；
    （2）求Sn=f（
    1
    n
    ）+f（
    2
    n
    ）+A+f（
    n-1
    n
    ）+f（
    n
    n
    ）
    （3）记Tn为数列{
    1
    (Sn+
    		2
    )(Sn+1+
    		2
    )
    }的前n项和，若Tn＜a（Sn+1+
    		2
    ）对一切n∈N*都成立，试求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设函数f（x）=
    2x
    2x+
    		2
    的图象上两点P1（x1，y1）、P2（x2，y2），若
    OP
    =
    1
    2
    （
    OP1
    +
    OP2
    ），且点P的横坐标为
    1
    2
    ．
    （1）求证：P点的纵坐标为定值，并求出这个定值；
    （2）求Sn=f（
    1
    n
    ）+f（
    2
    n
    ）+A+f（
    n-1
    n
    ）+f（
    n
    n
    ）
    （3）记Tn为数列{
    1
    (Sn+
    		2
    )(Sn+1+
    		2
    )
    }的前n项和，若Tn＜a（Sn+1+
    		2
    ）对一切n∈N*都成立，试求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ex-x（e为自然对数的底数）
    （Ⅰ）求f（x）的最小值；
    （Ⅱ）设不等式f（x）＞ax的解集为P，且{x|0≤x≤2}⊆P，求实数a的取值范围；
    （Ⅲ）设n∈N*，证明：(
    1
    n
    )n+(
    2
    n
    )n+…+(
    n-1
    n
    )n+(
    n
    n
    )n＜
    1
    1-e-1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设M=10a2+81a+207，P=a+2，Q=26-2a；若将lgM，lgQ，lgP适当排序后可构成公差为1的等差数列{an}的前三项．
    （1）试比较M、P、Q的大小；
    （2）求a的值及{an}的通项；
    （3）记函数f（x）=anx2+2an+1x+an+2（n∈N*）的图象在x轴上截得的线段长为bn，设Tn=
    1
    4
    (b1b2+b2b3+…+bn-1bn    ）（n≥2），求Tn，并证明T2T3T4…Tn＞
    2n-1
    n
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设M=10a2+81a+207，P=a+2，Q=26-2a；若将lgM，lgQ，lgP适当排序后可构成公差为1的等差数列{an}的前三项．
    （1）试比较M、P、Q的大小；
    （2）求a的值及{an}的通项；
    （3）记函数f（x）=anx2+2an+1x+an+2（n∈N*）的图象在x轴上截得的线段长为bn，设Tn=
    1
    4
    (b1b2+b2b3+…+bn-1bn    ）（n≥2），求Tn，并证明T2T3T4…Tn＞
    2n-1
    n
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）已知函数f(x)=aex，g(x)= lna-ln(x +1)（其中a为常数，e为自然对数底），函数y =f(x)在A(0，a)处的切线与y =g(x)在B(0，lna)处的切线互相垂直.

      (Ⅰ) 求f(x) ，g(x)的解析式；

      (Ⅱ) 求证：对任意n ÎN*，    f(n)+g(n)>2n；

      (Ⅲ) 设y =g(x-1)的图象为C1，h(x)=-x2+bx的图象为C2，若C1与C2相交于P、Q，过PQ中点垂直于x轴的直线分别交C1、C2于M、N，问是否存在实数b，使得C1在M处的切线与C2在N处的切线平行？说明你的理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）已知函数f(x)=aex，g(x)= lna-ln(x +1)（其中a为常数，e为自然对数底），函数y =f(x)在A(0，a)处的切线与y =g(x)在B(0，lna)处的切线互相垂直.

      (Ⅰ) 求f(x) ，g(x)的解析式；

      (Ⅱ) 求证：对任意n ÎN*，    f(n)+g(n)>2n；

      (Ⅲ) 设y =g(x-1)的图象为C1，h(x)=-x2+bx的图象为C2，若C1与C2相交于P、Q，过PQ中点垂直于x轴的直线分别交C1、C2于M、N，问是否存在实数b，使得C1在M处的切线与C2在N处的切线平行？说明你的理由.

    查看答案和解析>>


    同步练习册答案