练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设有一个回归直线方程为
    ?
    y
    =bx+2    ，变量x增加一个单位时，变量y平均减少2.5个单位，则当
    .
    x
    =1    时，直线必过定点（　　）
    A．（-2.5，2）B．（1，-0.5）C．（2.5，4.25）D．（1，4.5）
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    设有一个回归直线方程为
    ?
    y
    =bx+2    ，变量x增加一个单位时，变量y平均减少2.5个单位，则当
    .
    x
    =1    时，直线必过定点（　　）
    A、（-2.5，2）
    B、（1，-0.5）
    C、（2.5，4.25）
    D、（1，4.5）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设有一个回归直线方程为
    ?
    y
    =bx+2    ，变量x增加一个单位时，变量y平均减少2.5个单位，则当
    .
    x
    =1    时，直线必过定点（　　）
    A．（-2.5，2）B．（1，-0.5）C．（2.5，4.25）D．（1，4.5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•济宁二模）下列命题：
    ①线性回归方程对应的直线
    y
    =
    b
    x+
    a
    至少经过其样本数据点（x1，yl），（x1，yl），…，（xn，yn）中的一个点；
    ②设f（x）为定义在R上的奇函数，当x＞0时，f（x）=
    		x
    ．则当x＜0时，f（x）=
    		-x
    ；
    ③若圆x2+y2+Dx+Ey+F=0（D2+E2-4F＞0）与坐标轴的交点坐标分别为（x1，0），（x2，0），（0，yl），（0，y2），则x1x2-y1y2=0；
    ④若圆锥的底面直径为2，母线长为
    		2
    ，则该圆锥的外接球表面积为4π．
    其中正确命题的序号为．
    ③④
    ③④
    ．（把所有正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    某工业部门进行一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机选了10个企业做样本，资料见表．

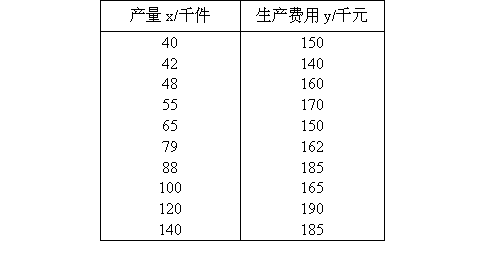
    由资料知，y对x有线性相关关系．

    (1)设回归直线方程为y=bx＋a，求系数a，b．

    (2)试估计产量为35000件时的生产费用．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    某工业部门进行一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机选了10个企业做样本，资料见表．

    由资料知，y对x有线性相关关系．

    (1)设回归直线方程为y=bx＋a，求系数a，b．

    (2)试估计产量为35000件时的生产费用．

    查看答案和解析>>

    科目：高中数学 来源：训练必修三数学人教A版 人教A版 题型：044

    某工业部门进行一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机抽取选了10个企业作样本，有如下资料：

    完成下列要求：

    (1)画出散点图，并判断它们是否有相关关系；

    (2)若y与x之间具有线性相关关系，设回归直线方程为y^＝bx＋a，求系数a、b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某工业部门进行一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机抽取选了10个企业作样本，有如下资料：

    产量（千件）

    40

    42

    48

    55

    65

    79

    88

    100

    120

    140

    生产费用（千元）

    150

    140

    160

    170

    150

    162

    185

    165

    190

    185

        完成下列要求：

        （1）画出散点图，并判断它们是否有相关关系;

        （2）若y与x之间具有线性相关关系，设回归直线方程为y^=bx+a，求系数a、b。

       

    查看答案和解析>>

    科目：高中数学 来源：选修设计数学1-2北师大版 北师大版 题型：013

    下列说法中错误的是

    [　　]

    A．如果变量η与ζ之间存在着线性相关关系，则我们根据实验数据得到的点(xi，yi)(i＝1，2，3，…n)将散布在某一条直线附近

    B．如果两个变量ζ与η之间不存在线性关系，那么根据实验数据不能写出一个线性方程

    C．设x、y是具有线性相关的两个变量，且回归直线方程是y＝bx＋a，则b叫回归系数

    D．为使求出的线性回归方程有意义，可用统计假设检验的方法判断变量ζ与η之间是否存在线性相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某工业部门进行了一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机提选了10个企业作样本，有如下资料：

    产量x（千件）

    40

    42

    48

    55

    65

    79

    88

    100

    120

    140

    生产费用y（千元）

    150

    140

    160

    170

    150

    162

    185

    165

    190

    185

    完成下列要求：

    （1）计算ｘ与ｙ的相关系数；

    （2）对这两个变量之间是否线性相关进行相关性检验；

    （3）设回归直线方程为=bx+a，求系数a,b.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法中错误的是(    )

    A.如果变量η与ξ之间存在着线性相关关系，则我们根据实验数据得到的点(xi,yi)(i=1,2, …,n)将散布在某一条直线的附近

    B.如果两个变量η与ξ之间不存在着线性相关关系，那么根据它们的一组数据(xi,yi)(i=1,2, …,n)不能写出一个线性方程

    C.设x,y是具有相关关系的两个变量，且x关于y的线性回归方程为=bx+a，b叫做回归系数

    D.为使求出的线性回归方程有意义，可用统计假设检验的方法来判定变量η与ξ之间是否存在线性相关关系

    查看答案和解析>>


    同步练习册答案