练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    曲线y=lnx在点（e，f（e））处的切线方程是（　　）
    A．x-ey=0B．x+ey=0C．x+ey-2e=0D．x-ey+2=0
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    曲线y=lnx在点（e，f（e））处的切线方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    曲线y=lnx在点（e，f（e））处的切线方程是（　　）
    A．x-ey=0B．x+ey=0C．x+ey-2e=0D．x-ey+2=0

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年浙江省杭州市富阳市场口中学高二（下）期中数学试卷（文科）（解析版） 题型：选择题

    曲线y=lnx在点（e，f（e））处的切线方程是（ ）
    A．x-ey=0
    B．x+ey=0
    C．x+ey-2e=0
    D．x-ey+2=0

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省中山一中高三（上）第四次统练数学试卷（理科）（解析版） 题型：解答题

    已知f（x）=ax-lnx，，A∈R．
    （Ⅰ）当x∈（0，e]时，f（x）的最小值是3，求a的值；
    （Ⅱ）记函数y=F（x）的图象为曲线C．设点A（x1，y1），B（x2，y2）是曲线C上的不同两点．如果在曲线C上存在点M（x，y），使得：①；②曲线C在点M处的切线平行于直线AB，则称函数F（x）存在“中值相依切线”．试问：函数G（x）=g（x）-f（x），是否存在“中值相依切线”，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省中山一中高三（上）第四次统练数学试卷（理科）（解析版） 题型：解答题

    已知f（x）=ax-lnx，，A∈R．
    （Ⅰ）当x∈（0，e]时，f（x）的最小值是3，求a的值；
    （Ⅱ）记函数y=F（x）的图象为曲线C．设点A（x1，y1），B（x2，y2）是曲线C上的不同两点．如果在曲线C上存在点M（x，y），使得：①；②曲线C在点M处的切线平行于直线AB，则称函数F（x）存在“中值相依切线”．试问：函数G（x）=g（x）-f（x），是否存在“中值相依切线”，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

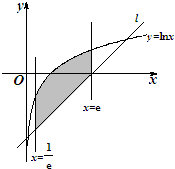    精英家教网由函数f（x）=xlnx-x的图象在点P（e，f（e））处的切线l与直线x=e-1，直线x=e（其中e是自然对数的底数）及曲线y=lnx所围成的曲边四边形（如图中的阴影部分）的面积S=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年江西省高考数学仿真押题卷11（文科）（解析版） 题型：解答题

    由函数f（x）=xlnx-x的图象在点P（e，f（e））处的切线l直线x=e-1，直线x=e（其中e是自然对数的底数）及曲线y=lnx所围成的曲边四边形（如图中的阴影部分）的面积S=______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=-lnx，x∈（0，e）．曲线y=f（x）在点（t，f（t））处的切线与x轴和y轴分别交于A、B两点，设O为坐标原点，求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnx，若g（x）=f（x）+
    2
    x
    +x-2-b（b∈R）．
    （1）求曲线y=f（x）在点P（1，f（1））处的切线方程；
    （2）若函数g（x）在区间[e-1，e]上有两个零点，求实数b的取值范围；
    （3）当0＜m＜n时，求证：f（m+n）-f（2n）＜
    m-n
    2n
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    a
    x
    +lnx-1（a是常数，e=2.71828）．
    （Ⅰ）若x=2是函数f（x）的极值点，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）当a=1时，方程f（x）=m在x∈[
    1
    e
    ，e2]上有两解，求实数m的取值范围；
    （Ⅲ）求证：ln
    n
    n-1
    ＞
    1
    n
    （n＞1，且n∈N*）．

    查看答案和解析>>


    同步练习册答案