练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当a＞0时，设命题P：函数f(x)=x+
    a
    x
    在区间（1，2）上单调递增；命题Q：不等式x2+ax+1＞0对任意x∈R都成立．若“P且Q”是真命题，则实数a的取值范围是（　　）
    A．0＜a≤1B．1≤a＜2C．0≤a≤2D．0＜a＜1或a≥2
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    当a＞0时，设命题P：函数f(x)=x+
    a
    x
    在区间（1，2）上单调递增；命题Q：不等式x2+ax+1＞0对任意x∈R都成立．若“P且Q”是真命题，则实数a的取值范围是（　　）
    A、0＜a≤1
    B、1≤a＜2
    C、0≤a≤2
    D、0＜a＜1或a≥2

    查看答案和解析>>

    科目：高中数学 来源：珠海二模 题型：单选题

    当a＞0时，设命题P：函数f(x)=x+
    a
    x
    在区间（1，2）上单调递增；命题Q：不等式x2+ax+1＞0对任意x∈R都成立．若“P且Q”是真命题，则实数a的取值范围是（　　）
    A．0＜a≤1B．1≤a＜2C．0≤a≤2D．0＜a＜1或a≥2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设命题p：函数f（x）=x2-2ax-1在区间[-1，1]内不单调；命题q：当x∈（0，+∞）时，不等式x2-ax+1＞0恒成立．如果命题p∨q为真命题，p∧q为假命题，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题P：函数f(x)=
    1
    3
    (1-x)    且|f（a）|＜2，命题Q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}且A∩B=∅，
    （1）分别求命题P、Q为真命题时的实数a的取值范围；
    （2）当实数a取何范围时，命题P、Q中有且仅有一个为真命题；
    （3）设P、Q皆为真时a的取值范围为集合S，T={y|y=x+
    m
    x
    ，x∈R，x≠0，m＞0}    ，若?RT⊆S，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知命题P：函数f(x)=
    1
    3
    (1-x)    且|f（a）|＜2，命题Q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}且A∩B=∅，
    （1）分别求命题P、Q为真命题时的实数a的取值范围；
    （2）当实数a取何范围时，命题P、Q中有且仅有一个为真命题；
    （3）设P、Q皆为真时a的取值范围为集合S，T={y|y=x+
    m
    x
    ，x∈R，x≠0，m＞0}    ，若?RT⊆S，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修1－1)　2009－2010学年　第16期　总第172期 人教课标版(A选修1－1) 题型：044

    设命题p：若y＝f(x)为单调增函数，则y＝f(ax)(a＞0，a≠1)也是单调增函数；命题q：存在实数a，使关于x的方程x2＋2x＋loga＝0无解．当p为真且q为假时，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：江西省新建二中2010届高三上学期第一次月考数学文科试题 题型：044

    设命题p：若y＝f(x)为单调增函数，则y＝f(ax)(a＞0，a≠1)也是单调增函数．命题q：存在实数a，使关于x的方程x2＋2x＋loga＝0的解集只有一个子集．当p或q有且只有一个正确时，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

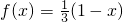    已知命题P：函数数学公式且|f（a）|＜2，命题Q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}且A∩B=∅，
    （1）分别求命题P、Q为真命题时的实数a的取值范围；
    （2）当实数a取何范围时，命题P、Q中有且仅有一个为真命题；
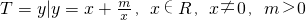    （3）设P、Q皆为真时a的取值范围为集合S，数学公式，若?RT⊆S，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a＞0，设命题p：函数y=(
    1
    a
    )x    为增函数．命题q：当x∈[
    1
    2
    ，2]时函数f(x)=x+
    1
    x
    ＞
    1
    a
    恒成立．如果p∨q为真命题，p∧q为假命题，求a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题：①函数f(x)=3sin(2x-
    π
    3
    )    的图象关于点(-
    π
    6
    ，0)    对称；②若a≥b＞-1，则
    a
    1+a
    ≥
    b
    1+b
    ；③存在实数x，使x3+x2+1=0；④设P（x1，y1）为圆O1：x2+y2=9上任意一点，圆O2：（x-a）2+（y-b）2=1，当（x1-a）2+（y1-b）2=1时，两圆相切．其中正确命题的序号是
     
    ．（把你认为正确的都填上）

    查看答案和解析>>


    同步练习册答案