已知{an}是等比数列,公比为q,设Sn=a1+a2Cn1+a3Cn2+…+an+1Cnn(其中n∈N*,n>2),且Tn=Cn0+Cn1+Cn2+…+Cnn(其中n∈N*,n>2),如果数列{}有极限,则公比q的取值范围是( )| A.-3<q≤1且q≠0 | B.-3<q<1且q≠0 | | C.-1<q≤1且q≠0 | D.-1<q<1且q≠0 |
|
相关习题
科目:高中数学
来源:
题型:
已知{a
n}是等比数列,公比为q,设S
n=a
1+a
2C
n1+a
3C
n2+…+a
n+1C
nn(其中n>2,n∈N
+),且S
n1=C
n0+C
n1+C
n2+…+C
nn,如果
存在,求公比q的取值范围.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知{a
n}是等比数列,公比为q,设S
n=a
1+a
2C
n1+a
3C
n2+…+a
n+1C
nn(其中n∈N
*,n>2),且T
n=C
n0+C
n1+C
n2+…+C
nn(其中n∈N
*,n>2),如果数列
{}有极限,则公比q的取值范围是( )
| A、-3<q≤1且q≠0 |
| B、-3<q<1且q≠0 |
| C、-1<q≤1且q≠0 |
| D、-1<q<1且q≠0 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知{a
n}是等比数列,公比为q,设S
n=a
1+a
2C
n1+a
3C
n2+…+a
n+1C
nn(其中n∈N
*,n>2),且T
n=C
n0+C
n1+C
n2+…+C
nn(其中n∈N
*,n>2),如果数列
{}有极限,则公比q的取值范围是( )
| A.-3<q≤1且q≠0 | B.-3<q<1且q≠0 |
| C.-1<q≤1且q≠0 | D.-1<q<1且q≠0 |
查看答案和解析>>
科目:高中数学
来源:2005-2006学年浙江省杭州二中高三(上)1月月考数学试卷(理科)(解析版)
题型:选择题
已知{a
n}是等比数列,公比为q,设S
n=a
1+a
2C
n1+a
3C
n2+…+a
n+1C
nn(其中n∈N
*,n>2),且T
n=C
n+C
n1+C
n2+…+C
nn(其中n∈N
*,n>2),如果数列
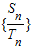
有极限,则公比q的取值范围是( )
A.-3<q≤1且q≠0
B.-3<q<1且q≠0
C.-1<q≤1且q≠0
D.-1<q<1且q≠0
查看答案和解析>>
科目:高中数学
来源:高考数学一轮复习必备(第85课时):第十章 排列、组合和概率-二项式定理(2)(解析版)
题型:解答题
已知{a
n}是等比数列,公比为q,设S
n=a
1+a
2C
n1+a
3C
n2+…+a
n+1C
nn(其中n>2,n∈N
+),且S
n1=C
n+C
n1+C
n2+…+C
nn,如果

存在,求公比q的取值范围.
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知{an}是等比数列,公比为q,设Sn=a1+a2Cn1+a3Cn2+…+an+1Cnn(其中n∈N*,n>2),且Tn=Cn0+Cn1+Cn2+…+Cnn(其中n∈N*,n>2),如果数列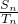 有极限,则公比q的取值范围是
有极限,则公比q的取值范围是
- A.
-3<q≤1且q≠0
- B.
-3<q<1且q≠0
- C.
-1<q≤1且q≠0
- D.
-1<q<1且q≠0
查看答案和解析>>
科目:高中数学
来源:
题型:
已知{a
n}是等比数列,公比q>1,前n项和为
Sn,且=,a4=4,
数列{bn}满足:bn=.
(1)求数列{a
n},{b
n}的通项公式;
(2)设数列{b
nb
n+1}的前n项和为T
n,求证
≤Tn<(n∈N*).
查看答案和解析>>
科目:高中数学
来源:安徽模拟
题型:解答题
已知{a
n}是等比数列,公比q>1,前n项和为
Sn,且=,a4=4,数列bn满足:=2,n=1,2,…(1)求数列{a
n},{b
n}的通项公式;
(2)设数数{b
nb
n+1}的前n项和为T
n,求证
≤Tn<(n∈N*).
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省济宁市泗水一中高三(上)12月月考数学试卷(理科)(解析版)
题型:解答题
已知{a
n}是等比数列,公比q>1,前n项和为

,

.
(1)求数列{a
n},{b
n}的通项公式;
(2)设数列{b
nb
n+1}的前n项和为T
n,求证

.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省济宁市泗水一中高三(上)12月月考数学试卷(理科)(解析版)
题型:解答题
已知{a
n}是等比数列,公比q>1,前n项和为
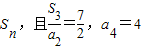
,
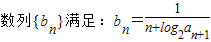
.
(1)求数列{a
n},{b
n}的通项公式;
(2)设数列{b
nb
n+1}的前n项和为T
n,求证
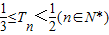
.
查看答案和解析>>

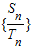 有极限,则公比q的取值范围是( )
有极限,则公比q的取值范围是( ) 存在,求公比q的取值范围.
存在,求公比q的取值范围.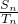 有极限,则公比q的取值范围是
有极限,则公比q的取值范围是 ,
, .
. .
.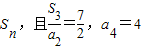 ,
,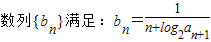 .
.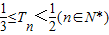 .
.