求过点P(3,2),并与直线x+4y-2=0垂直的直线的方程为( )| A.x-4y-11=0 | B.x+4y-11=0 | C.4x+y-10=0 | D.4x-y-10=0 |
|
相关习题
科目:高中数学
来源:
题型:
6、求过点P(3,2),并与直线x+4y-2=0垂直的直线的方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
求过点P(3,2),并与直线x+4y-2=0垂直的直线的方程为( )
| A.x-4y-11=0 | B.x+4y-11=0 | C.4x+y-10=0 | D.4x-y-10=0 |
查看答案和解析>>
科目:高中数学
来源:2010-2011学年山东省济南市章丘一中高一(下)期中数学试卷(解析版)
题型:选择题
求过点P(3,2),并与直线x+4y-2=0垂直的直线的方程为( )
A.x-4y-11=0
B.x+4y-11=0
C.4x+y-10=0
D.4x-y-10=0
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
求过点P(3,2),并与直线x+4y-2=0垂直的直线的方程为
- A.
x-4y-11=0
- B.
x+4y-11=0
- C.
4x+y-10=0
- D.
4x-y-10=0
查看答案和解析>>
科目:高中数学
来源:2011-2012学年北京市东城区示范校高三(下)3月联考数学试卷(理科)(解析版)
题型:解答题
直线
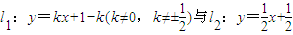
相交于点P.直线l
1与x轴交于点P
1,过点P
1作x轴的垂线交直线l
2于点Q
1,过点Q
1作y轴的垂线交直线l
1于点P
2,过点P
2作x轴的垂线交直线l
2于点Q
2,…,这样一直作下去,可得到一系列点P
1,Q
1,P
2,Q
2,…,点P
n(n=1,2,…)的横坐标构成数列{x
n}.
(1)当k=2时,求点P
1,P
2,P
3的坐标并猜出点P
n的坐标;
(2)证明数列{x
n-1}是等比数列,并求出数列{x
n}的通项公式;
(3)比较
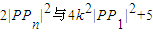
的大小.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知直线x+ky-3=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为8.
(1)求椭圆C的标准方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1.试证明:当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交,并求直线l被圆O所截得的弦长L的取值范围.
查看答案和解析>>
科目:高中数学
来源:
题型:
一直线经过P(3,2),并且和两条直线x-3y+10=0与2x-y-8=0都相交,且两交点连线的中点为P,求这条直线的方程.
查看答案和解析>>
科目:高中数学
来源:杭州一模
题型:解答题
已知直线x+ky-3=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为8.
(1)求椭圆C的标准方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1.试证明:当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交,并求直线l被圆O所截得的弦长L的取值范围.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省杭州高级中学高三(下)第六次月考数学试卷(文科)(解析版)
题型:解答题
已知直线x+ky-3=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为8.
(1)求椭圆C的标准方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1.试证明:当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交,并求直线l被圆O所截得的弦长L的取值范围.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年四川省成都市望子成龙学校高二(下)期中数学模拟试卷(解析版)
题型:解答题
已知直线x+ky-3=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为8.
(1)求椭圆C的标准方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1.试证明:当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交,并求直线l被圆O所截得的弦长L的取值范围.
查看答案和解析>>

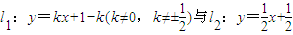 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.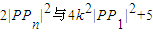 的大小.
的大小.