
△ABC中,∠C=90°,a=3,b=4,若△ABC三边长都增加1,则新三角形最大角的余弦值为( )
|
科目:高中数学 来源:2010年三峡三中高一下学期期末考试(文科)数学卷 题型:选择题
三棱锥P—ABC中,若PA⊥平面ABC,∠ACB=90°,那么在三棱锥的侧面和底面中,直角三角形的个数为
A.4个 B. 3个 C. 2个 D. 1个
科目:高中数学 来源:不详 题型:单选题
| A.4个 | B.3个 | C.2个 | D.1个 |
科目:高中数学 来源:江西省莲塘一中2010-2011学年高二上学期期末终结性测试数学理科试题 题型:013
下列命题中真命题的个数为:
①命题“若x2+y2=0,则x,y全为0”的逆命题;
②命题“全等三角形是相似三角形”的否命题;
③命题“若m>0,则x2+x-m=0有实根”的逆否命题;
④命题“在△ABC中,a、b、c分别是角A、B、C所对的边长,若∠C=90°,则c2=a2+b2”的逆否命题.
1
2
3
4
科目:高中数学 来源:2010年福建省高二第二学期半期考试数学(理科)试题 题型:选择题
对于直角坐标平面内的任意两点A(x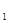 ,
, y
y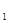 )、B(x
)、B(x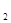 ,y
,y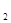 ),定义它们之间的一种“距离”:
),定义它们之间的一种“距离”:
‖AB‖=︱x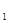 -x
-x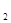 ︱+︱y
︱+︱y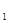 -y
-y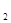 ︱。给出下列三个命题:
︱。给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖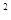 +‖CB‖
+‖CB‖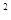 =‖AB‖
=‖AB‖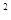 ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
科目:高中数学 来源: 题型:
| BC |
| AC |
科目:高中数学 来源:不详 题型:解答题
| BC |
| AC |
科目:高中数学 来源:必修二训练数学北师版 北师版 题型:013
已知A、B、C是球O面上的三点,则下列命题中,真命题的个数是
①若AB=6,AC=8,BC=10,OA=10,则O到平面ABC的距离是5![]()
②若∠BAC=90°,E是BC中点,AE=4,OE=3,则OA=5
③若∠BAC=60°,BC=4,OB=![]() ,则O到平面ABC的距离是
,则O到平面ABC的距离是![]()
④若E是△ABC的BC边上的中点且OE⊥平面ABC,则△ABC不一定是直角三角形
A.1
B.2
C.3
D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com