
在等差数列{an}中,若m+n=p+q(m,n,p∈N*)),则下列各式一定成立的是( )
|
科目:高中数学 来源: 题型:
| A、am+an=ap+aq | ||||
| B、am-an=ap-aq | ||||
| C、am.an=ap.aq | ||||
D、
|
科目:高中数学 来源:不详 题型:单选题
| A.am+an=ap+aq | B.am-an=ap-aq | ||||
| C.am.an=ap.aq | D.
|
科目:高中数学 来源:2010-2011学年海南省海口市洋浦中学高一(下)第一次月考数学试卷(解析版) 题型:选择题

科目:高中数学 来源: 题型:单选题
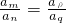
科目:高中数学 来源:上海高考真题 题型:解答题
科目:高中数学 来源:上海高考真题 题型:解答题
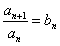 ,并说明理由;
,并说明理由;科目:高中数学 来源:2013-2014学年广东省佛山市南海区高三(上)入学摸底数学试卷(理科)(解析版) 题型:填空题
 .类比上述结论,对于等比数列{bn}(bn>0,n∈N*),若bm=r,bn=s(n-m≥2,m,n∈N*),则可以得到bm+n= .
.类比上述结论,对于等比数列{bn}(bn>0,n∈N*),若bm=r,bn=s(n-m≥2,m,n∈N*),则可以得到bm+n= .科目:高中数学 来源: 题型:
| nq-mp |
| n-m |
| n-m |
| ||
| n-m |
| ||
科目:高中数学 来源:不详 题型:填空题
| nq-mp |
| n-m |
科目:高中数学 来源: 题型:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com