给出下面结论:
①命题p:“?x∈R,x2-3x+2≥0”的否定为?p:“?x∈R,x2-3x+2<0”;
②命题:“?x∈M,P(x)”的否定为:“?x∈M,P(x)”;
③若?p是q的必要条件,则p是?q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件.
其中正确结论的个数为( ) |
相关习题
科目:高中数学
来源:信阳模拟
题型:单选题
给出下面结论:
①命题p:“?x∈R,x
2-3x+2≥0”的否定为?p:“?x∈R,x
2-3x+2<0”;
②命题:“?x∈M,P(x)”的否定为:“?x∈M,P(x)”;
③若?p是q的必要条件,则p是?q的充分条件;
④“M>N”是“㏒
aM>㏒
aN”的充分不必要条件.
其中正确结论的个数为( )
查看答案和解析>>
科目:高中数学
来源:2012年河南省信阳市高三第二次调研数学试卷(理科)(解析版)
题型:选择题
给出下面结论:
①命题p:“?x∈R,x2-3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”;
②命题:“?x∈M,P(x)”的否定为:“?x∈M,P(x)”;
③若¬p是q的必要条件,则p是¬q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件.
其中正确结论的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:2012年安徽师大附中高考数学四模试卷(理科)(解析版)
题型:选择题
给出下面结论:
①命题p:“?x∈R,x2-3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”;
②命题:“?x∈M,P(x)”的否定为:“?x∈M,P(x)”;
③若¬p是q的必要条件,则p是¬q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件.
其中正确结论的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
给出下面结论:
①命题p:“?x∈R,x2-3x+2≥0”的否定为?p:“?x∈R,x2-3x+2<0”;
②命题:“?x∈M,P(x)”的否定为:“?x∈M,P(x)”;
③若?p是q的必要条件,则p是?q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件.
其中正确结论的个数为
- A.
4
- B.
3
- C.
2
- D.
1
查看答案和解析>>
科目:高中数学
来源:安徽省师大附中2012届高三第四次模拟考试数学理科试题
题型:013
给出下面结论:
①命题p:“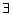 x∈R,x2-3x+2≥0”的否定为
x∈R,x2-3x+2≥0”的否定为 p:“
p:“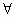 x∈R,x2-3x+2<0”;
x∈R,x2-3x+2<0”;
②命题:“ x∈M,P(x)”的否定为:“
x∈M,P(x)”的否定为:“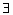 x∈M,P(x)”;
x∈M,P(x)”;
③若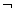 p是q的必要条件,则
p是q的必要条件,则
p是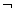 q的充分条件;
q的充分条件;
④“M>N”是“logaM>logaN”的充分不必要条件.
其中正确结论的个数为
[ ]
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省汕头市高三(上)期末数学试卷(文科)(解析版)
题型:选择题
给出下面结论:
①命题p:“?x
∈R,x
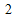
-3x
+2≥0”的否定为¬p:“?x∈R,x
2-3x+2<0”
②函数f(x)=2
x+3x的零点所在区间是(-1,0);
③函数y=sin2x的图象向左平移

个单位后,得到函数
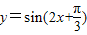
图象;
④对于直线m,n和平面α,若m⊥α,m⊥n,则n∥α.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学
来源:2013年广东省高考数学模拟试卷(文科)(解析版)
题型:选择题
给出下面结论:
①命题p:“?x
∈R,x
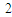
-3x
+2≥0”的否定为¬p:“?x∈R,x
2-3x+2<0”
②函数f(x)=2
x+3x的零点所在区间是(-1,0);
③函数y=sin2x的图象向左平移
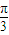
个单位后,得到函数

图象;
④对于直线m,n和平面α,若m⊥α,m⊥n,则n∥α.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学
来源:
题型:
给出下面结论:
①命题p:“?x
0∈R,x
-3x
0+2≥0”的否定为¬p:“?x∈R,x
2-3x+2<0”
②函数f(x)=2
x+3x的零点所在区间是(-1,0);
③函数y=sin2x的图象向左平移
个单位后,得到函数
y=sin(2x+)图象;
④对于直线m,n和平面α,若m⊥α,m⊥n,则n∥α.
其中正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
给出下面结论:
①命题p:“?x
0∈R,x
-3x
0+2≥0”的否定为¬p:“?x∈R,x
2-3x+2<0”
②函数f(x)=2
x+3x的零点所在区间是(-1,0);
③函数y=sin2x的图象向左平移
个单位后,得到函数
y=sin(2x+)图象;
④对于直线m,n和平面α,若m⊥α,m⊥n,则n
∥α.
其中正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
给出下面结论:
①命题p:“?x0∈R,x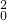 -3x0+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”
-3x0+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”
②函数f(x)=2x+3x的零点所在区间是(-1,0);
③函数y=sin2x的图象向左平移 个单位后,得到函数
个单位后,得到函数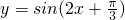 图象;
图象;
④对于直线m,n和平面α,若m⊥α,m⊥n,则n∥α.
其中正确结论的个数是
- A.
1
- B.
2
- C.
3
- D.
4
查看答案和解析>>

![]() x∈R,x2-3x+2≥0”的否定为
x∈R,x2-3x+2≥0”的否定为![]() p:“
p:“![]() x∈R,x2-3x+2<0”;
x∈R,x2-3x+2<0”;![]() x∈M,P(x)”的否定为:“
x∈M,P(x)”的否定为:“![]() x∈M,P(x)”;
x∈M,P(x)”;![]() p是q的必要条件,则
p是q的必要条件,则![]() q的充分条件;
q的充分条件;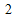 -3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”
-3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0” 个单位后,得到函数
个单位后,得到函数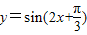 图象;
图象;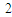 -3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”
-3x+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”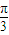 个单位后,得到函数
个单位后,得到函数 图象;
图象;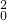 -3x0+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0”
-3x0+2≥0”的否定为¬p:“?x∈R,x2-3x+2<0” 个单位后,得到函数
个单位后,得到函数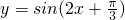 图象;
图象;