
已知点P(x,y),其中x∈{1,2},y∈{1,3,4},则在同一直角坐标系中所确定的不同点的个数是( )
|
科目:高中数学 来源:2012-2013学年湖南省长沙市浏阳一中高二(下)第一次月考数学试卷(理科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 2 |
| |PF2|+|QF2| |
| |PF2|•|QF2| |
| ||
| 2 |
| 1 |
| 2 |
| PA |
| PF2 |
| 7 |
| 7 |
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:填空题
| x2 |
| 4 |
| 2 |
| |PF2|+|QF2| |
| |PF2|•|QF2| |
| ||
| 2 |
| 1 |
| 2 |
| PA |
| PF2 |
| 7 |
| 7 |
科目:高中数学 来源: 题型:
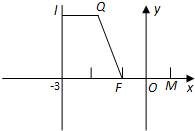 已知点Q(x,y)位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.
已知点Q(x,y)位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.| FP |
| 1 |
| 2 |
| FA |
| FB |
| EP |
| AB |
科目:高中数学 来源:2013年四川省达州市万源三中高考数学模拟试卷(理科)(解析版) 题型:填空题
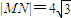 ;
; ,则抛物线E上一定存在两点关于直线y=-x+b对称.
,则抛物线E上一定存在两点关于直线y=-x+b对称.科目:高中数学 来源: 题型:
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com