Question

18．图中是两个正方形，大正方形的边长是8厘米，小正方形的边长是5厘米，大正方形的一个顶点正好是小正方形的中心，求阴影部分的面积．

Answer 1

分析 如图点O是正方形的中心，连接OA、OB，就可以证明△BOD≌△AOC，就可以得到四边形ACOB的面积=△AOB的面积，求出三角形AOB的面积就可以了．

解答 解：如图，设点O是正方形的中心，连接OA、OB，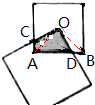

∴OA=OB，∠AOB=90°．
∴∠OAB=∠OBA=45°
∴∠OAC=45°，
∴∠OAC=∠OBD
∵AB=5，在Rt△AOB中，由勾股定理得：
AO=BO=$\frac{5}{2}\sqrt{2}$，
∴S_△AOB=$\frac{\frac{5}{2}\sqrt{2}×\frac{5}{2}\sqrt{2}}{2}$=$\frac{25}{4}$．
∵∠BOC=90°，
∴∠BOC=∠AOB，
∴∠COA=∠DOB．
在△AOC和△BOD中，
$\left\{\begin{array}{l}{∠OAC=∠OBD}\\{OA=OB}\\{∠AOC=∠BOD}\end{array}\right.$，
∴△AOC≌△BOD，
∴S_△AOC=S_△BOD，
∴S_{四边形ACOD}=S_△AOB，
∴S_{四边形ACOD}=$\frac{25}{4}$（平方厘米）．
答：阴影部分的面积为$\frac{25}{4}$平方厘米．

点评 本题考查了正方形的性质，勾股定理的运用，三角形的面积公式的运用，全等三角形的判定及性质．在解答中灵活运用图形转化是关键．