
 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,(1)求证:B′E=BF;(2)设AE=a,AB=b,BF=c,试猜想a、b、c之间有何等量关系,并给予证明.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,(1)求证:B′E=BF;(2)设AE=a,AB=b,BF=c,试猜想a、b、c之间有何等量关系,并给予证明.


 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:
| 2 |

| 2 |
查看答案和解析>>
科目:小学数学 来源: 题型:
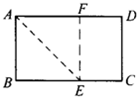 如图,一张矩形纸片,要折叠出一个最大的正方形纸,小明把矩形的一个角沿折痕翻折上去,使AB边和AD边上的AF重合,则四边形ABEF就是一个最大的正方形,他的判定方法是
如图,一张矩形纸片,要折叠出一个最大的正方形纸,小明把矩形的一个角沿折痕翻折上去,使AB边和AD边上的AF重合,则四边形ABEF就是一个最大的正方形,他的判定方法是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com