
����Ŀ�����л��������������¼�ơ���������2017��10��1����ʩ�С���Ϊ��Ŀ�ƪ֮��������������ÿ���˵�һ��ϢϢ���.ij����Ϊ�˵��б��������ǶԸ÷��ɵ��˽�����������ȡ50�ˣ����ǵ����䶼������[25��85]�ϣ������Ƶ�ʷֲ����˽⡶�������������±���
���� | [25��35) | [35��45) | [45��55) | [55��65) | [65��75) | [75��85) |
Ƶ�� | 5 | 5 | 10 | 15 | 5 | 10 |
�˽⡶������ | 1 | 2 | 8 | 12 | 4 | 5 |
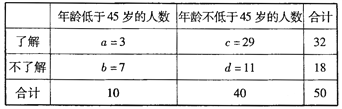
������д����2��2 �����������ж��Ƿ���99%�İ�����Ϊ��45��Ϊ�ֽ����˽⡶�����������в��죻

��������������[45��55����[65��75���ı��������и����ѡȡ2�˽���������У���ѡ�е�4���в��˽⡶����������ΪX�����������X�ķֲ��к���ѧ����.

���𰸡���������������������������.
����������������������ݱ����������ݿɵ����������������������ù�ʽ�����![]() �����ٽ�ֵ�Ƚϼ��ɵý��ۣ�����
�����ٽ�ֵ�Ƚϼ��ɵý��ۣ����� ![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() �������������֪ʶ��Ϲŵ�����ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�
�������������֪ʶ��Ϲŵ�����ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�![]() ����ѧ����.
����ѧ����.
���������������д����2��2 �����������ж��Ƿ���99%�İ�����Ϊ��45��Ϊ�ֽ����˽⡶�����������в��죻

��������������[45��55����[65��75���ı��������и����ѡȡ2�˽���������У���ѡ�е�4���в��˽⡶����������ΪX�����������X�ķֲ��к���ѧ����.
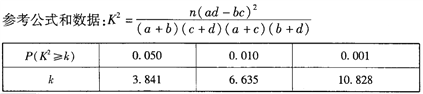
�⣺����2��2��������
![]()
![]() û��99%�İ�����Ϊ��45��Ϊ�ֽ����˽⡶�����������в���.
û��99%�İ�����Ϊ��45��Ϊ�ֽ����˽⡶�����������в���.
������X�����п���ȡֵΪ0��1��2��3��
![]()
![]()
![]()
![]()
��X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
����X����ѧ������![]()


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��д������
49+24=
![]() +
+![]() =
=
24��8=
390��0=
700��6=
800��310=
43��7=
640+90=
13��7=
1��![]() =
=
509��5��
295��3��
35��7+15=
8��9��32=
5+4��6=
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ӵ�С��˳�����У���ȷ���ǣ�������
A.0.087��0.807��0.8��0.78 B.0.807��0.8��0.78��0.087
C.0.8071��0.8��0.087��0.78 ��
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��д���������:
ʮ����______�� ʮ����______�� ��ʮ��______��
��ʮ��______�� ��ʮ����______�� ʮ����______����
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ����400���Ͻ���200�����ܣ���������ǰ�Բ���뾶Ϊ36�ף�ÿ���ܵ���1.2�ף���4�����1���������� ����
A��1.21��
B��2.4��
C��3.6��
D��36��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com